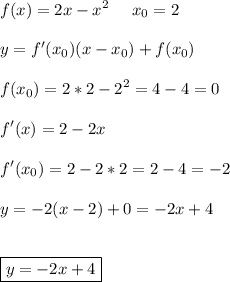
у=f(a)+f'(a)*(x-a)- уравнение касательной к графику y=f(x) в точке с абсциссой x=a,
f(a)=2*a-a²
f(2)=2*2-2²=0
f'(x)=2-2x
f'(a)=2-2a
f'(2)=2-2*2=-2
у=f(2)+f'(2)*(x-2)
у=0-2*(х-2)
у=-2х+4
(1; 4); (4; 1)
{ x√x + y√y = 9
{ x√y + y√x = 6
Переходим к новым переменным
a = √x; x = a^2; x√x = a^3
b = √y; y = b^2; y√y = b^3
{ a^3 + b^3 = 9
{ a^2*b + ab^2 = 6
Умножим второе уравнение на 3
{ a^3 + b^3 = 9
{ 3a^2*b + 3ab^2 = 18
Складываем уравнения
a^3 + b^3 + 3a^2*b + 3ab^2 = 9 + 18
Слева записан куб суммы
(a + b)^3 = 27
a + b = 3
b = 3 - a
Подставляем
a^2*(3 - a) + a(3 - a)^2 = 6
a(3 - a)(a + 3 - a) = 6
3a(3 - a) = 6
a(3 - a) = 2
-a^2 + 3a = 2
a^2 - 3a + 2 = 0
(a - 1)(a - 2) = 0
1) a = 1; b = 2
x = a^2 = 1; y = b^2 = 4
(1; 4) - это решение.
2) a = 2; b = 1
x = a^2 = 4; y = b^2 = 1
(4; 1) - это решение.
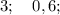
Объяснение:
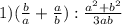
1. Сначала выполним сложение в скобках. Общий знаменатель двух дробей:
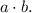
Дополнительный множитель для первой дроби:
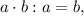
Дополнительный множитель для второй дроби:

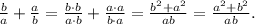
2. Деление на дробь равносильно умножению на обратную дробь:
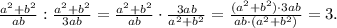
ответ: 3.
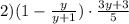
1. Сначала выполним вычитание в скобках. Единицу представим как дробь со знаменателем 1:
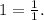
Общий знаменатель двух дробей:
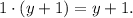
Дополнительный множитель для первой дроби:
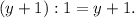
Дополнительный множитель для второй дроби:
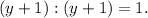
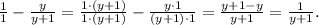
2. Вынесем тройку за скобки в числителе второй дроби:
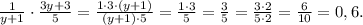
ответ: 0,6.