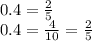
Решить систему линейных уравнений методом подстановки и методом сложения:
{
y
+
2
x
=
1
y
−
x
=
3
Решение методом подстановки.
{
y
+
2
x
=
1
y
−
x
=
3
⇒
{
y
=
−
2
x
+
1
y
−
x
=
3
⇒
{
y
=
−
2
x
+
1
(
−
2
x
+
1
)
−
x
=
3
⇒
{
y
=
−
2
x
+
1
−
3
x
−
2
=
0
⇒
{
y
=
−
2
x
+
1
x
=
−
2
3
⇒
{
y
=
7
3
x
=
−
2
3
y
=
2
1
3
;
x
=
−
2
3
Решение методом сложения.
{
y
+
2
x
=
1
y
−
x
=
3
Вычитаем уравнения:
−
{
y
+
2
x
=
1
y
−
x
=
3
(
y
+
2
x
)
−
(
y
−
x
)
=
1
−
3
3
x
=
−
2
x
=
−
2
3
Подставиим найденную переменную в первое уравнение:
(
−
2
3
)
+
2
x
=
1
y
=
7
3
y
=
2
1
3
;
x
=
−
2
3
Объяснение:
х км/ч скорость катера
(х + 1,5) км/ч скорость катера по течению
(х - 1,5) км/ч скорость катера против течения
2(х+1,5) км катер по течению реки за 2 часа
3(х-1,5) км катер против течения реки за 3 часа
По условию известно, что за 2 часа катер проходит по течению реки в 1.25 раза меньше ,чем за 3 часа против течения реки.
Получаем уравнение:
1,25 * 2(х+1,5) = 3(х-1,5)
2,5(х+1,5) = 3х - 4,5
2,5х + 3,75 = 3х - 4,5
3х - 2,5х = 8,25
0,5х = 8,25
х = 8,25 6 0,5
х = 16,5
ответ. 16,% км/ч скорость катера в стоячей воде
Да, твоя версия правильная.
4/10=2/5