
Объяснение:
Решите графически систему уравнений.
y=6/x
x-y=1
y=6/x - гипербола :
x 1 2 3 -1 -2 -3
y 6 3 2 -6 -3 -2
x-y=1
-x+y=-1
y=-1+x - линейная функция ,
x 0 1
y -1 0
y=6/x
y=-1+x
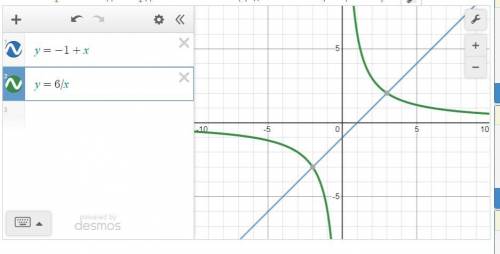
Как видим по графику , точки пересечения такие: (3;2) и (-2;-3)
3 нулями
Объяснение:
По определению N!=1·2·3·...·(N-1)·N.
Поэтому
16!=1·2·3·...·15·16.
Задачу можно решить несколькими
В результате произведения двух чисел получаем нуль, если один из них чётное число, а другой оканчивается на 5. Среди чисел от 1 по 16 есть такие числа как 5 и 15, которые при умножении на чётные числа как 2 и 4 дадут по нулю.
Так как в произведении участвует 10, то получим ещё один ноль. Число 16! оканчивается всего 3 нулями.
По формуле количества нулей N!
K(N!) = [N/5]+[N/25]+[N/125]+..., где [ х ] - целая часть числа х.
Так как N=16 и [16/25]=0, то последующие слагаемые также равны нулю. Тогда
K(16!) = [16/5]+0=3+0=3.
(-2; -3) ;(3; 2)
в файле: построить графики функций по точкам( точка пересечения гиперболы с прямой- решение системы)