Question

Я питался , но выходит не понятно что заранее)))

Answer 1

$x + y = 8 \\ {x}^{2} - 3 {y}^{2} = 24$

$x = 8 - y \\ {(8 - y)}^{2} - 3 {y}^{2} = 24 \\ 64 - 16y + {y}^{2} - 3 {y}^{2} = 24 \\ - 2 {y}^{2} - 16y + 40 = 0 \\ {y}^{2} + 8y - 20 = 0 \\ d = 64 + 80 = 144 = {12}^{2} \\ y1 = \frac{ - 8 + 12}{2} = \frac{4}{2} = 2 \\ y2 = \frac{ - 8 - 12}{2} = \frac{ - 20}{2} = - 10$

Теперь подставляем значения у в первую формулу

$x1 = 8 - y1 \\ x1 = 8 - 2= 6$

$x2 = 8 - y2 \\ x2 = 8 + 10 = 18$

ответ: (6 , 2) ; (18 , -10)

Answer 2

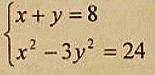
Во второе уравнение подставим у=8-х, который выразили из первого.

х²-3*(8-х)²=24, решим второе уравнение. х²-3*(64-16х+х²)=24

х²-192+48х-3х²-24=0; 2х²-48х+216=0;х²-24х+108=0

х₁,₂=12±√(144-108)=12±6; х₁=18; х₂=6, тогда у₁=8-18=-10; у₂=8-6=2

ответ (18;-10); (6:2)