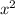
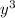 z(14-2x-3y-z) В области x,y,z >0
z(14-2x-3y-z) В области x,y,z >0ответ: х = 2; у = 2
Объяснение:
Решить систему уравнений
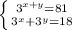
Решение
В первом уравнении 81 можно заменить на 81 =9·9=3²·3² = 3⁴
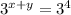
х + у = 4
Запишем систему уравнений
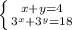
Выразим переменную y из первого уравнения и подставим во второе уравнение
y = 4 - x
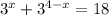
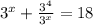
заменим переменные t = 3ˣ
t + 81/t = 18
Так как t = 0 не является корнем данного уравнения умножим обе части уравнения на t.
t² - 18t + 81 = 0
(t-9)² = 0
t = 9
Сделаем обратную замену и найдем переменную х
3ˣ = 9
3ˣ = 3²
х = 2
Найдем значение переменной у
у = 4 - х = 4 - 2 = 2
5.4) 15 (минут) - за столько времени наполнят бассейн обе трубы, открытые одновременно.
5.2) 15/20, или 3/4.
Объяснение:
5.4 - Первая труба наполнит бассейн за 24 мин, а вторая за 40 мин. За сколько минут наполнится бассейн, если открыть обе эти трубы?
1 - объём бассейна.
1:24=1/24 - часть бассейна заполнит первая труба за 1 минуту.
1:40=1/40 - часть бассейна заполнит вторая труба за 1 минуту.
1/24+1/40=8/120=1/15 - часть бассейна заполнят обе трубы за 1 минуту, открытые одновременно.
1 : 1/15=15 (минут) - за столько времени наполнят бассейн обе трубы, открытые одновременно.
5.2 - Укажите хотя бы одну обыкновенную дробь, большую 0,7, но меньшую 0,8 .
Чтобы определить обыкновенную дробь, которая будет меньше, чем 0,8, и больше, чем 0,7, переведём десятичные дроби 0,7 и 0,8 в обыкновенные дроби.
0,7 = 7/10;
0,8 = 8/10.
Теперь, пользуясь основным свойством дроби, умножим числитель и знаменатель получившихся обыкновенных дробей на число 2.
7/10 = 14/20;
8/10 = 16/20.
Поскольку знаменатели у дробей одинаковые, то для сравнения дробей используем их числители.
14 < 15 < 16.
Дробь с числителем 15 и знаменателем 20 будет удовлетворять условиям задания.
ответ: 15/20, или 3/4.
Второй вариант:
Если добавить ноль к 0,7 и к 0,8 то они не изменятся, и мы получим
0,70 и 0,80, но между ними можно поставить число, например, 0,75.
Но так как в задаче сказано ОБЫКНОВЕННУЮ дробь, переводим
десятичную дробь в обыкновенную, получаем 3/4, (или 15/20).
ответ: 128 , при x=y=z=2
Объяснение:
u=z*x^2*y^3*(14-2x-3y-z) , где x,y,z>0
Очевидно, раз нам нужно наибольшее значение, то нам есть смысл рассматривать только те значения, при которых 14-2x-3y-z>=0
0<2x+3y+z<=14
В рассматриваемой области из неравенства Коши-Буняковского имеем :
z*x^2*y^3 = z*x*x*y*y*y<= ( (2x+3y+z)/6)^6
Откуда:
u<=6^(-6) * ( (2x+3y+z))^6 *(14-(2x+3y+z) )
Пусть : 2x+3y+z=t
0<t<=14
Найдем максимум функции:
f(t) = t^6 *(14-t) =14t^6 -t^7
Найдем нули производной:
f'(t) = 84t^5-7*t^6 = 0
t1=0
84-7t=0
t2=84/7 = 12 - точка максимума.
f(14)=f(0)=0
f(12) = 2*12^6 - максимальное значение на 0<t<=14
Таким образом:
u<=6^(-6) * ( (2x+3y+z))^6 *(14-(2x+3y+z) ) <= 6^(-6) *2*12^6 = 2^7 = 128. Иначе говоря, umax = 128
Данное значение будет получено, когда:
x=y=z ( требование выполнения равенства в неравенстве Коши-Буняковского), и когда 2x+3y+z = 12 или 6x=12 → x=y=z=2