Question

Задано функцію f(x)=x-1/x . 1. Побудуйте графік функції y=f(x). 2. Знайдіть похідну функції f(x) . 3. Запишіть рівняння дотичних до графіка функції y=f(x), які паралельні прямій y=x4 . 4. Знайдіть найменше значення функції x−f(x) на проміжку [1/2;∞) .

Answer 1

Все в объяснениях.

Объяснение:

1. Постройте график функции y=f(x).

$f(x)=\frac{x-1}{x} =\frac{x}{x} -\frac{1}{x} \\f(x)=-\frac{1}{x} +1$

Гипербола, полученная сдвигом графика у=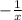$-\frac{1}x}$ на 1 вверх по оу. у(-2)=0,5 ;у(-1)=1 ;у(-2)=0,5 ;у(2)=-0,5 ;у(1)=-1 ;у(2)=-0,5

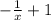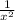2. f '(x)= ( $-\frac{1}{x} +1$ ) ' =$\frac{1}{x^{2} }$  .

3. Уравнения касательной y =к (x −x₀)+f (x₀) .

Прямая y=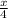$\frac{x}{4}$ ,  к=1\4.

Найдем точку касания      

$\frac{x}{4} =\frac{x-1}{x} \\x^{2} -4x+4=0$

(x-2)²=0  , x=2.  

f (2)=-1\2+1=0,5

y =0,25* (x −2)+0,5

у=0,25х

Вторая касательная пройдет через х=-2

f (-2)=1\2+1=1,5

y =0,25* (x −2)+1,5

у=0,25х+1

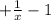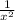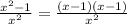4. Наименьшее значение функции у'=(x−f(x) ) '=(х$+\frac{1}{x} -1$)' =      

=1 -$\frac{1}{x^{2} }$=$\frac{x^{2}-1 }{x^{2} }=\frac{(x-1)(x-1) }{x^{2} }$  .

у'=0 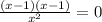  ,  $\frac{(x-1)(x-1) }{x^{2} }=0$   ,х=1  ,   х=-1.

На промежутке [1/2;∞) лежит только х=1

у'______[1\2] - - - - -(1)+ + + + +

y                          ↓              ↑

x=1 точка минимума.

Наименьшее значение может быть при х=1\2 или х=1:

у(1\2) =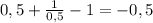$0,5+\frac{1}{0,5} -1=-0,5$  .

у(1)= 1+1-1=1.

Наименьшее значение  функции х-f(x) равно -0,5