пусть а, a+d, a+2d - три числа, образующие арифмитическую прогрессию, тогда
a+8, a+d, a+2d - три числа образующие геометричесскую прогрессию
отсюда и из условия имеем
a+8+a+d+a+2d=26 (условие задачи - сумма членов геометричесской прогрессии равна 26)
3a+3d=18
a+d=6 (*)
d=6-a
(a+d)^2=(a+8)(a+2d) (использовано свойство, если дано три последовательные члены геометрической прогрессии, то квадрат среднего равен произведению первого и третьего члена)
6^2=(a+8)(12-a) (используем (*) )
36=12a+96-a^2-8a
a^2-4a-60=0
D=256=16^2
a1=(4+16)/2=10
a2=(4-16)=-6
b[1]=a=10
b[2=]a+d=6
q=b[2]/b[1]=6/10=0.6
или
b[1]=a=-6
b[2]=a+d=6
q=b[2]/b[1]=6/(-6)=-1
сумма всех натуральных чисел от 45 до 90 это сумма арифмитической прогрессии с первым членом a[1]=45, последним членом a[n]=90 и разницей арифмиттиеческой прогрессии d=1
по формуле общего члена найдем количевство членов
a[n]=a[1]+(n-1)*d
90=45+(n-1)*1
45=n-1
n=45+1=46
по формуле суммы
S=(a[1]+a[n])/2* n
S=(45+90)/2 *46=3 105
б) сумма всех целых чисел от -100 до -65 это сумма арифмитической прогрессии с первым членом a[1]=-100, последним членом a[n]=-65, и разницей арифмитичесской прогрессии d=1
по формуле общего члена найдем количевство членов
a[n]=a[1]+(n-1)*d
-65=-100+(n-1)*1
35=n-1
n=35+1=36
по формуле суммы
S=(a[1]+a[n])/2* n
S=(-100+(-65))/2 *36=-2 970
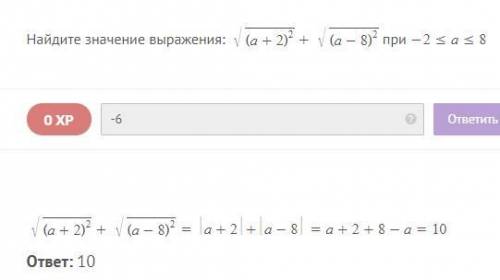
В данном случае, степень корня и показатель степени сокращаются. При сокращении корня, число/выражение извлекается со знаком модуля. Итак, получилось:
|a+2|+|a-8|
В условие сказано, что:
-2_<а_<8
(_< - меньше или равно)
Теперь раскрываем модули:
а+2+8-а
Объясняю, почему "8-а", а не "а-8". Так как значение а меньше или равно восьми, мы меняем знаки. Ведь если вместо а подобрать число меньше 8, ответ будет с отрицательным знаком. Но мы же знаем, что при раскрытии модулей, ответ должен быть положительным. А заменять в данном случае знак "-" на "+" мы не можем:
а+8 - неверно!
Вот поэтому и меняем знаки. Получается:
а+2-а+8
-а и а сокращаются, 2+8=10
ответ: 10