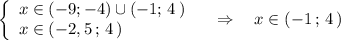
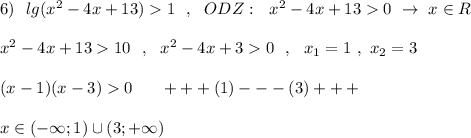
![7)\ \ log_{0,5}(1+x-\sqrt{x^2-4})0\\x^2-4\geq 0\end{array}\right\ \ \left\{\begin{array}{l}\sqrt{x^2-4}-2,5\\x-1\\x\in (-\infty ;-2\, ]\cup [\, 2\, ;+\infty )\end{array}\right\\\\\\x\in [\, 2\, ;+\infty )](/tpl/images/1358/7877/38d48.png)
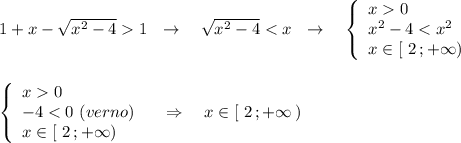
ответ:Нам нужно разложить на множители выражение ac - ad - 5bc + 5bd для этого сгруппируем попарно первое со вторым и третье с четвертым слагаемые и вынесем общий множитель за скобки.
ac - ad - 5bc + 5bd = (ac - ad) - (5bc - 5bd);
Из первой скобки вынесем a, а из второй 5b, получим:
(ac - ad) - (5bc - 5bd) = a(c - d) - 5b(c - d).
Рассмотрим полученное выражение. В результате мы получили разность двух выражений каждое из которых содержит скобку (c - d), вынесем ее как общий множитель.
a(c - d) - 5b(c - d) = (с - d)(a - 5b).
ответ: (с - d)(a - 5b).
Объяснение: