Question

Найти сумму всех целых a из промежутка [-3;15], при которых функция f(x)=lg((x²+3)×㏒0,5 a - 2x(2-㏒2 a)+4x²+6) определена на всей числовой оси объясните подробно у log числа 0,5 и 2 основания

Answer 1

6

Объяснение:

Область определения функции: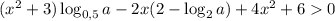 $(x^2+3)\log_{0{,}5}{a}-2x(2-\log_{2}{a})+4x^2+60$. Неравенство должно выполняться для любого x, в частности для x = 0. Подставим это значение:

$3\log_{0{,}5}a+60\\\log_{0{,}5}{a}-2\\0$

Значит, потенциально подходящие значения a = 1, 2, 3. Необходимо проверить каждое из них, чтобы удостовериться, что неравенство справедливо для всех x. Приведём левую часть к стандартному виду квадратного трёхчлена:

$(\log_{0,5}{a}+4)x^2-2(2-\log_{2}{a})x+6+3\log_{0{,}5}{a}0\\(4-\log_{2}{a})x^2-2(2-\log_2{a})x+6-3\log_{2}{a}0$

Так как a не превосходит 3, старший коэффициент положителен, ветви параболы направлены вверх. Значит, чтобы неравенство выполнялось для всех x, дискриминант левой части (или в данном случае удобно использовать D/4) должен быть отрицательным:

$D_{/4}=(2-\log_{2}{a})^2-(4-\log_{2}{a})(6-3\log_{2}{a})=-2\log_2^2{a}+14\log_2{a}-20$

Пусть $\log_2{a}=t, 1\leq a\leq 3\Rightarrow 0\leq t$.

$D_{/4}=-2t^2+14t-20$

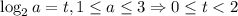Все t подходят, а значит, и все a. Сумма подходящих a — 1 + 2 + 3 = 6.