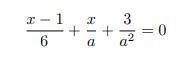
Дискриминант определяет :
1) есть ли корни у данного уравнения и сколько их
если D<0, то корней нет
D> то есть два корня уравнения
D=0 , то корень 1
2) Когда строим график квадратичной функции, то найдя дискриминант понимаем есть ли перечения параболы с осью х и в скольки точках:
если D<0, то парабола лежит либо выше оси абсцисс( если при х² положительный коэффициент и ветви параболы направлены вверх), либо ниже оси ОХ (если при х² отрицательное число и ветви параболы будут направлены вниз)
при D>0 на оси абсцисс( ось ОХ) лежат две точки параболы( значение корней - абсциссы этих точек)
при D=0 - на осы абсцисс лежит вершина параболы.
3) если найдём дискриминант и корни , то квадратный трёхчлен раскладывается на множители
ах²+bx+ c=a(x- x₁)(x-x₂), где x₁,x₂- корни
Искомая функция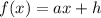 
.
Найдем значения искомой функции в заданных точках х:
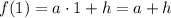
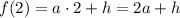
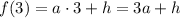
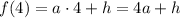
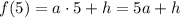
Кроме этого, для каждого из аргументов есть еще и экспериментальное значение, которое обозначим через функцию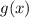 
:
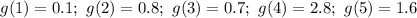
Составим функцию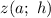 
, которая будет суммировать квадраты разностей значений функций 
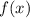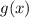и соответствующих аргументов:
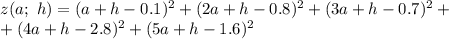
Исследуем эту функцию на экстремум.
Найдем частные производные:
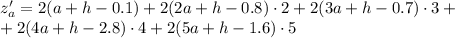
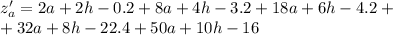
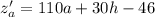
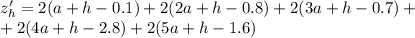
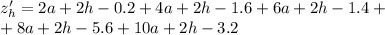
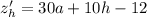
Необходимое условие экстремума: равенство нулю частных производных:
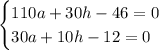
Домножим второе уравнение на (-3):
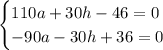
Складываем уравнения:
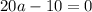
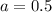
Подставим значение а во второе уравнение исходной системы:
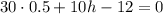
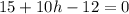
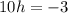
Точка (0.5; -0.3) - предполагаемая точка экстремума.
Найдем вторые частные производные функции:
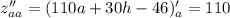
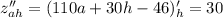
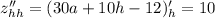
Рассмотрим выражение:
Так как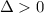 
и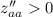 
, то точка (0.5; -0.3) является точкой минимума.
Значит, в точке (0.5; -0.3) функция 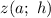имеет минимум.
Тогда, значения 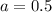и есть искомые коэффициенты функции .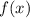
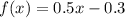
ответ: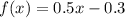
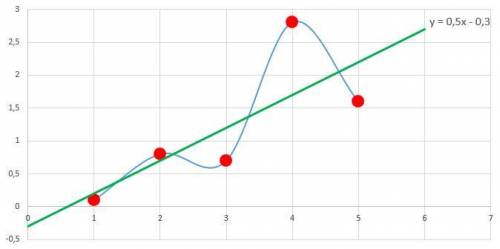
(Сначала по привычке подумал, что квадратное уравнение получится, соре)