6. Какая точность при округлении десятичных дробей до тысячных ?

👇

Увидеть ответ

Ответ:

tim152

21.06.2021

при соблюдении правил округления 0.0005

4,5(81 оценок)

Открыть все ответы

Ответ:

Ananasik3333

21.06.2021

1 формула сложения

Cos (x+п/6) = cosx * cos(п/6) – sinx*sin(п/6)=1/2 cosx - √3/2sinx

2 формула двойного угла

Sinx=4/5 ; cos2x = 1- sin2x = 1-(4/5)2 =1-16/25=9/25 ; cosx =3/5

Sin2x = 2*sinx*cosx =2*4/5*3/5=24/25

3 формула двойного /тройного угла

-sina /(sin2a*sin3a) =

=-sin(3a-2a) /(sin2a*sin3a) =

=- (ctg2a – ctg3a) = ctg3a – ctg2a

4 11x =8x+3x ; 5x =8x -3x

sin11x +sin5x =2*1/2 (sin(8x+3x)+sin(8x-3x)) =2*sin8x*cos3x

5 формула двойного угла

(ctg^2(п/8)-1) / (2ctg(п/8)) = ctg (2*п/8) = ctg (п/4)=ctg 45o =1

4,6(20 оценок)

Ответ:

Shabalina04

21.06.2021

Отыщем область значений указанной функции.
Для этого сначала преобразуем определённым образом подкоренное выражение для удобства: раскроем скобки, затем дважды используем формулу понижения степени, приведя выражение к квадратному трёхчлену относительно некоторой функции.

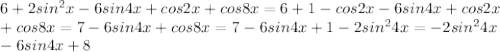
$6 + 2 sin^{2} x - 6sin4x + cos2x + cos 8x = 6 + 1 - cos2x - 6sin4x + cos2x \\ + cos 8x = 7 - 6sin4x + cos8x = 7 - 6sin4x + 1 - 2 sin^{2} 4x = -2 sin^{2} 4x \\ - 6sin 4x + 8$
Таким образом, мы смогли привести подкоренное выражение к квадратному трёхчлену относительно sin4x. На всякий случай скажу, что в препоследнем равенстве с формулы понижения степени я выразил квадрат синуса через косинус удвоенного угла.

Теперь всё сводится к нахождению наименьшего и наибольшего значений полученного трёхчлена. Если мы сделаем замену t = sin 4x, то получаем квадратный трёхчлен
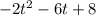
$-2 t^{2} - 6t + 8$
, ветви соответствующей параболы которого направлены вниз в силу отрицательности коэффициента при квадрате. Найдём её абсциссу оси симметрии:
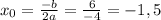$x_{0} = \frac{-b}{2a} = \frac{6}{-4} = -1,5$ . Следовательно, квадратичная функция правее оси симметрии монотонно убывает, то есть, при $t \ \textgreater \ -1,5$ . Поэтому большему значению функции соответствует меньшее значение аргумента. В частности, это происходит и на отрезке [-1,1]

. Почему этот отрезок важен, так потому, что вспоминаем, что t - это у нас не переменная сама по себе, а синус, который принимает значения именно из указанного отрезка.

Итак, на отрезке [-1,1] квадратный трёхчлен относительно t убывает, поэтому наименьшее его значение достигается в правом конце(в точке 1), а наибольшее - в левом(в точке -1). То есть,
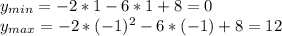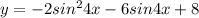$y_{min} = -2 * 1 - 6 * 1 + 8 = 0 \\ y_{max} = -2 * (-1)^{2} - 6 * (-1) + 8 = 12$ , где $y = -2 sin^{2} 4x - 6sin4x + 8$ .
То есть, E(y) = [0, 12]

.

А тогда квадратный корень из этого выражения(в силу своей монотонности), даёт $[0, \sqrt{12} ]$ .
Теперь считаем, какие целые числа входят в полученную область значений.
0, 1, 2, 3 - и всё. Их ровно 4.

4,4(76 оценок)

Это интересно:

Стиль-и-уход-за-собой

16.06.2021

Как нарисовать дизайн ногтей Splatter...

Компьютеры-и-электроника

29.08.2022

Как быстро и легко изменить язык Google...

Компьютеры-и-электроника

05.08.2021

Секреты успешной презентации: Как создать эффективную презентацию в PowerPoint?...

Стиль-и-уход-за-собой