N2
а) 3x+12>0 3x>-12 x>-4
2x-3<0 2x<3 x<1,5 x∈(-4;1,5)
б) 3x+2>2x-3 x>-5
x-5>0 x>5 x∈(5;+∞)
N3
a)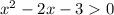 
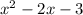=0
x1+x2=2 x1=3
x1
x2=-3 x2=-1
(x-3)(x+1)>0
+ +
_____._______._____
-1 - 3
x∈(-∞;-1)∪(3;+∞).
б)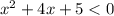 
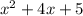=0
d=(4)²-415=16-20=-4
нет решений
в)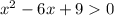 
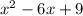=0
(x-3)²=0
(x-3)(x-3)>0
+
_____._____
3 - x∈(-∞;3)
(2;-2), (-2;-2)
Объяснение:
x²-4=y²+4y+4
x²-(y+2)²=4
(x-y-2)(x+y+2)=4
[x-y-2 + x+y+2=2x - число четное => четность (x-y-2) и (x+y+2) совпадает] => Т.к. 4=2², возможны 2 случая:
[1] {x-y-2=2, {x+y+2=2;
{x-y=4, {x+y=0;
{x=2, {y=-2;
[2] {x-y-2=-2, {x+y+2=-2;
{x-y=0, {x+y=-4;
{x=-2, {y=-2;