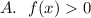 для любых
для любых  . Значит верно утверждение "Неравенство
. Значит верно утверждение "Неравенство  не имеет решений" (№3).
не имеет решений" (№3).
 для любых
для любых  . Значит, верно утверждение "Неравенство
. Значит, верно утверждение "Неравенство 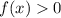 верно для любых "х", за исключением одной точки" ( эта точка касания оси ОХ и параболы, в ней
верно для любых "х", за исключением одной точки" ( эта точка касания оси ОХ и параболы, в ней  ) .
) .
 Функция
Функция 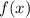 принимает как положительные , так и отрицательные значения, а также значения, равные 0 . Причём
принимает как положительные , так и отрицательные значения, а также значения, равные 0 . Причём 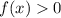 при
при 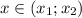 . Значит верно утверждение "
. Значит верно утверждение " 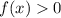 имеет решением интервал " .
имеет решением интервал " .
 при
при  . Значит верно утверждение "Неравенство
. Значит верно утверждение "Неравенство  верно при любом х" ( в этом неравенстве должно выполняться: или
верно при любом х" ( в этом неравенстве должно выполняться: или  или
или  ).
).
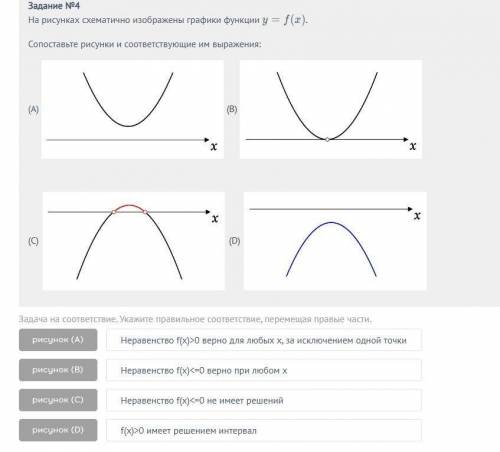
1. рис А -условие f(x)>0 для любых х
2. рис В -условие f(x)>0 для любых х, кроме одной точки
3. рис С -условие f(x)>0 имеет решением интервал
4. рис Д -условие fkx)<0 при любом х