1) Для представления в виде степени выражения -m^9, мы можем записать его в виде (-1)^9 * m^9. Так как (-1) в степени 9 равно -1, а m^9 остается без изменений, ответ будет: -m^9.
2) Выражение 16*x^4*y^4 уже представлено в виде степени. Каждый множитель 16, x^4 и y^4 уже является степенью соответствующей переменной. Поэтому ответ остается таким же: 16*x^4*y^4.
3) Чтобы представить выражение -27/125*p^3*q^3 в виде степени, мы можем записать его в виде (-3/5)^3 * p^3 * q^3. Так как (-3/5) в степени 3 остается (-3/5)^3, а p^3 и q^3 остаются без изменений, ответ будет: -27/125*p^3*q^3.
Все ответы представлены в виде степени, где числитель и знаменатель не содержат степени, а переменные остаются в степени, указанной в исходном выражении.
Для того чтобы доказать, что при всех натуральных значениях n выражение кратно 7, мы должны показать, что оно делится на 7 без остатка. Давайте разобъем задачу на несколько шагов:
Шаг 1: Упростить выражение
Так как это деление, мы можем применить правила деления степеней с одинаковым основанием, и выражение станет:
Шаг 2: Представить выражение в виде произведения
Мы можем разделить числитель и знаменатель на 7, так как это поможет нам показать, что выражение кратно 7. Тогда выражение будет:
Шаг 3: Докажите, что части выражения кратны 7
Мы знаем, что 22 делится на 7 без остатка, так как 7 * 3 = 21, а 22 = 21 + 1. То есть - кратно 7.
Теперь рассмотрим степенные части. Мы можем применить правила степеней и выражение станет:
Мы также можем сократить x в числителе и знаменателе, чтобы упростить выражение:
Теперь мы видим, что часть выражения является кратной 7. Для этого важно заметить, что число 15 делится на 7 без остатка, так как 7 * 2 = 14, а 15 = 14 + 1.
Поэтому весьма вероятно, что выражение кратно 7 при всех натуральных значениях n.
Однако, чтобы доказать это абсолютно уверенно, нам нужно провести более формальное доказательство, используя математические индукции или другие методы.
ответ: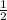
Объяснение:
Продолжение: