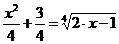
2sin2x + 3sinxcosx - 3cos2x = 1;
Представим 1 в виде суммы по основному тригонометрическому тождеству:
sin2x + 3cosxsinx - 3cos2x = sin2x + cos2x;
Приведем подобные:
sin2x + 3cosxsinx - 4cos2x = 0;
Разделим каждый член уравнения на cos2x:
tg2x + 3tgx - 4 = 0;
Произведем замену и решим квадратное уравнение:
t2 + 3t - 4 = 0;
D = 9 + 16 = 25;
t = (-3 +- 5)/2;
t1 = -4, t2 = 1;
Сделаем обратную замену:
tgx = 1; x = pi/4 + pin, n из Z;
tgx = -4; x = arctg(-4) pin, n из Z.
ответ: pi/4 + pin, n из Z; arctg(-4) pin, n из Z.
Объяснение:
Оцени!
Дробь не имеет смысла если её знаменатель равен нулю т.к. на ноль делить нельзя.
\dfrac{x}{x-4} ;\; x-4=0;\; \bold{x=4} dfrac{2b^2-9}{b(b-5)} ;\; b(b-5)=0;\; \bold{b=\{0;5\}}.
Дробь равна нулю если числитель равен нулю, а знаменатель - не равен.
\dfrac{x+1}{x} =0;\; \begin{Bmatrix}x+1=0\\x\ne 0\end{matrix} \\\begin{Bmatrix}x=-1\\x\ne 0\end{matrix} \qquad \bold{x=-1}dfrac{x(x-2)^2 }{x-2} =0;\; \begin{Bmatrix}x(x-2)^2 =0\\x-2\ne 0\end{matrix} \\\begin{Bmatrix}x=\{0;2\}\\x\ne 2\end{matrix} \qquad \bold{x=0}.
Объяснение:
удачи получить хорошую отметку
x=1
Объяснение:
рассмотрим функцию:
2x-1≥0 ⇔ x≥0.5
Её область определения: D(f)=[0.5;+∞)
Исследуем ее с производной:
Находим нули числителя:
Замечаем, что слева стоит возрастающая функция, справа - убывающая. Поэтому если и есть корень, то он единственный!
Не трудно догадаться, что корнем будет x=1
Теперь находим нули знаменателя:
метод интервалов с учетом D(f)
(0,5)---[1]---->ₓ
С пробных точек узнаем знаки промежутков и получаем:
(0,5)---[1]+++>ₓ
На интервале (0,5;1) производная отрицательна, значит функция убывает.
На интервале (1;+∞) производная положительна, значит функция возрастает
Таким образом x=1 - точка минимума и в том числе точка наименьшего значения функции
f(1)=0 - минимум и наименьшее значение функции
Таким образом мы выяснили, что f(x)≥0 при всех допустимых x, а равенство f(x)=0 достигается только в точке x=1 (в точке минимума)