![{x}^{3}+3x+2\sqrt[3]{x-4}-34=0](/tpl/images/3782/9411/beb22.png)
При a=-2 неравенство ax^2-(8+2a^2)x+16a>0 не имеет решений
Объяснение:
Выражение слева при а≠0 представляет собой параболу (при а=0 - решение есть).
Определим, при каких а у=ax^2-(8+2a^2)x+16a пересекает ось ОХ
Найдем дискриминант для ax^2-(8+2a^2)x+16a=0
D=(8+2а²)²-4а*16a=(8+2а²)²-(8а)²=(8+2а²-8а)(8+2а²+8а)=4(а-2)²(а+2)²=4(а²-4)²
D≥0 при любых значениях а, т. е. точки пересечения(хотя бы одна) с осью ОХ есть всегда.
Парабола будет лежать ниже оси ОХ в случае, когда а<0(ветви вниз направлены) и D=0(одна точка пересечения с осью ОХ)
4(а²-4)²=0; а²-4=0; a=-2
При a=-2 неравенство ax^2-(8+2a^2)x+16a>0 не имеет решений
Объяснение:
Выражение слева при а≠0 представляет собой параболу (при а=0 - решение есть).
Определим, при каких а у=ax^2-(8+2a^2)x+16a пересекает ось ОХ
Найдем дискриминант для ax^2-(8+2a^2)x+16a=0
D=(8+2а²)²-4а*16a=(8+2а²)²-(8а)²=(8+2а²-8а)(8+2а²+8а)=4(а-2)²(а+2)²=4(а²-4)²
D≥0 при любых значениях а, т. е. точки пересечения(хотя бы одна) с осью ОХ есть всегда.
Парабола будет лежать ниже оси ОХ в случае, когда а<0(ветви вниз направлены) и D=0(одна точка пересечения с осью ОХ)
4(а²-4)²=0; а²-4=0; a=-2
Запишем уравнение в виде:
Пусть левая и правая часть равны у. Тогда получим систему:
Рассмотрим каждое уравнение как функцию.
Графически возрастающая и убывающая функция могут пересекаться не более чем в одной точке.
В данном случае, понимая, что и область определения и область значений каждой функции представляют собой все действительные числа можно сказать, что такое пересечение обязательно произойдет.
Таким образом, если найден некоторый корень этого уравнения, то других корней у уравнения нет.
Подберем корень. Удобно начать проверку с "красивых значений". Например, будем выбирать х так, чтобы под знаком корня получался куб некоторого целого числа.
Пусть![\sqrt[3]{x-4} =\sqrt[3]{0}](/tpl/images/1360/1028/d91f8.png) , то есть
, то есть 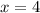 . Проверим, является ли это число корнем:
. Проверим, является ли это число корнем:
Пусть![\sqrt[3]{x-4} =\sqrt[3]{1}](/tpl/images/1360/1028/7bd4a.png) , то есть
, то есть 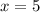 . Проверим, является ли это число корнем:
. Проверим, является ли это число корнем:
Пусть![\sqrt[3]{x-4} =\sqrt[3]{-1}](/tpl/images/1360/1028/4572f.png) , то есть
, то есть 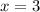 . Проверим, является ли это число корнем:
. Проверим, является ли это число корнем:
Таким образом, уравнение имеет единственный корень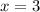
ответ: 3