==============================
Объяснение:
ответ: не менее 96 метров.
Объяснение:
Ширина дороги 6 м. Скорость пешехода 4,5 км/ч. На каком расстоянии от пешехода должен находиться автомобиль, который движется со скоростью 72 км/ч, чтобы пешеход успел спокойно перейти дорогу?
Решение.
Найдем время движения пешехода
4.5 км/час = 4,5 *1000м/час= 4500/3600 м/с=1,25 м/с
S=vt; 6=1,25t.
1.25t=6;
t=6 : 1.25 = 4.8 с необходимо пешеходу чтобы перейти дорогу.
72 км/час = 72*1000 м/час = 72 000/3600=м/с=20 м/с.
S =vt = 20*4,8=96 метров;
Автомобиль должен находиться на расстоянии более 96 метров.
(ab – a – 4)² + (ab – b – 3)² = 0
В левой части равенства находится сумма квадратов. Поскольку никакое действительное число при возведении в квадрат не может дать отрицательный результат, слагаемые в левой части либо нулевые, либо положительные. В таком случае сумма этих слагаемых равна нулю только тогда, когда каждое из слагаемых равно нулю.
Получаем систему из двух уравнений:
ab – a – 4 = 0
ab – b – 3 = 0
Из первого уравнения выразим b=(a + 4)/a и подставим полученное значение во второе уравнение:
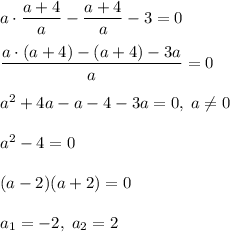
Подставим полученные значения a в первое уравнение и найдем b:
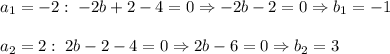
ответ: a₁ = –2, b₁ = –1; a₂ = 2, b₂ = 3.
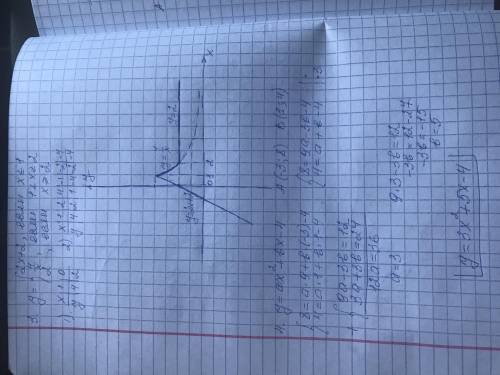
Задание 3
График построен, во вложениях.
Чтобы построить у себя график по этой картинке и функции, сначала построим первый кусочек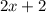 - прямая.
- прямая.
Для этого надо выбрать две точки. Первая точка будет для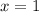 , как для граничного значения. Вторая при
, как для граничного значения. Вторая при 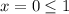 .
.
Получили точки (1; 4), (0; 2). Откладываем эти точки на координатной плоскости и проводим луч от (1; 4) через точку (0; 2).
Теперь перейдем к 3 кусочку - прямой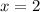 . Он задан от
. Он задан от 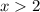 . Это прямая, параллельная оси OX. Ставим точку граничного условия (2; 2), выбираем любой
. Это прямая, параллельная оси OX. Ставим точку граничного условия (2; 2), выбираем любой 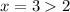 получаем вторую точку (3; 2). Проводим луч от (2; 2) через (3; 2).
получаем вторую точку (3; 2). Проводим луч от (2; 2) через (3; 2).
Осталось провести гиперболу между (1; 4) и (2; 2), делаем её похожей на картинку во вложениях.
Задание 4
Поставляем точки в выражение и получаем систему: