Question

ЕГЭ профильная математика, С3 решить систему неравенств. Заранее

Answer 1

$\left(\dfrac{1}{4};\;\dfrac{1}{3}\right]$

Объяснение:

Рассмотрим сначала первое неравенство системы.

Начнем с ОДЗ:

$log_3^2x+10,\;=\;x0\\log_3x+30,\;x\dfrac{1}{27}\\x0\\x+5\ne0,\;=\;x\ne-5\\=x\in\left(\dfrac{1}{27};+\infty\right)$

Продолжим решение:

$\dfrac{lg(log_3^2x+1)-lg(log_3x+3)}{x+5}\ge0\\\dfrac{lg\left(\dfrac{log_3^2x+1}{log_3x+3}\right)}{x+5}\ge0$

1)

$lg\left(\dfrac{log_3^2x+1}{log_3x+3}\right)=0,\;=\;\dfrac{log_3^2x+1}{log_3x+3}=1\\\\=log_3^2x+1=log_3x+3,\;=\;log_3^2x-log_3x-2=0$

Замена: $t=log_3x$.

$t^2-t-2=0\\t^2+t-2t-2=0\\t(t+1)-2(t+1)=0\\(t+1)(t-2)=0\\t=-1\\t=2$

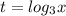Обратная замена:

$log_3x=-1\\x=\dfrac{1}{3}\\\\log_3x=2\\x=9$

С учетом ОДЗ оба корня подходят.

2)

$x+5\ne0\\x\ne-5$

С учетом ОДЗ получим, что решение неравенства:

$x\in\left(\dfrac{1}{27};\;\dfrac{1}{3}\right]\cup[9;\;+\infty)$

Теперь перейдем ко второму неравенству системы:

Понятно, что сначала нужно написать ОДЗ.

$0.5x0,\;=\;x0\\(0.5x)^{6^x}0,\;=\;x0\\=x0$

Продолжим решение:

$36^x+36\sqrt[4]{6}-6^{x+\frac{1}{4}}$

Заметим, что данное неравенство хорошо раскладывается на множители:

$36^x+36\sqrt[4]{6}-6^{x+\frac{1}{4}}$

Решим неравенство по методу интервалов.

1)

$\sqrt[4]{6}-6^x=0\\6^x=6^{\frac{1}{4}}\\x=\dfrac{1}{4}$

2)

$36-6^x-log_60.5x=0\\log_60.5x=-6^x+36$

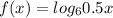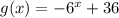Введем функции $f(x)=log_60.5x$ и $g(x)=-6^x+36$. Заметим, что первая функция возрастает, а вторая убывает. Поэтому, если уравнение имеет корень, он единственный. Теперь заметим, что x=2 - корень уравнения. Действительно, 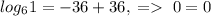$log_61=-36+36,\;=\;0=0$, верно. Так, мы решили это уравнение, получив, что его корень x=2.

Тогда решение неравенства с учетом ОДЗ:

$x\in\left(\dfrac{1}{4};\;2\right)$

Итого имеем:

$x\in\left(\dfrac{1}{27};\;\dfrac{1}{3}\right]\cup[9;\;+\infty)\\x\in\left(\dfrac{1}{4};\;2\right)$

Найдем пересечение:

$x\in\left(\dfrac{1}{4};\;\dfrac{1}{3}\right]$

Задание выполнено!