1.а) Область определения находим из системы неравенств
х+44>0; 2х-22>0;
х>-44;х>22/2⇒x∈(11;+∞).
4а) ㏒₃(х-4)+㏒₃(х+7)=㏒₃26; ОДЗ уравнения х больше 4, (х-4)(х+7)=26;
х²+7х-4х-28-26=0; х²+3х-54=0; По теореме, обратной теореме Виета, х₁=-9∉ОДЗ, не является корнем. х₂=6
4в) ㏒²₂х-㏒₂х-30=0; ОДЗ уравнения х∈(0;+∞) Пусть ㏒₂х=у, тогда у²-у-30=0; по теореме, обр. теореме Виета, у₁=-5; у₂=6 тогда ㏒₂х=-5; х=2⁻⁵; х=1/32 -входит в ОДЗ, корень.
㏒₂х=6; х=2⁶=64- входит в ОДЗ, корень.
5а)㏒₁/₅(22х-2)≥0
ОДЗ неравенства 22х-2>0; x>1/11
Заменим 0=㏒₁/₅1, т.к. основание логарифма меньше 1, то 22х-2≤1
22х≤3; х≤3/22; с учетом ОДЗ решением неравенства будет х∈(1/11;3/11)
в низу
Объяснение:
1. Перетворіть вираз з(ь – 6, 5) у такий, що тотожно дорівнює йому. 2. Запишіть вираз т – (6-n+b) без дужок. 3. Спростіть вираз 15-(a-4). 4. Розкрийте дужки й зведіть подібні доданки у виразі 4b – (76 + 2). 5. Виконайте тотожне перетворення виразу 2,5 (2k + 4а – 2). 6. Спростіть вираз 2(a+1) +а та знайдіть його значення, якщо a=1. 7. Доведіть тотожність (2x +1)-(1-2x) = 4х. 8. Зведіть подібні доданки у виразі -4+32+62. 9. Спростіть вираз -(-5)-(-y). 10. Доведіть, що вираз 7(a-b)+7(b – а) тотожно дорівнює 0. 11. Доведіть тотожність -(2-(-x)+2+x = 0. 12. Доведіть, що сума виразів 13c + 3 і 2c +3 ділиться на
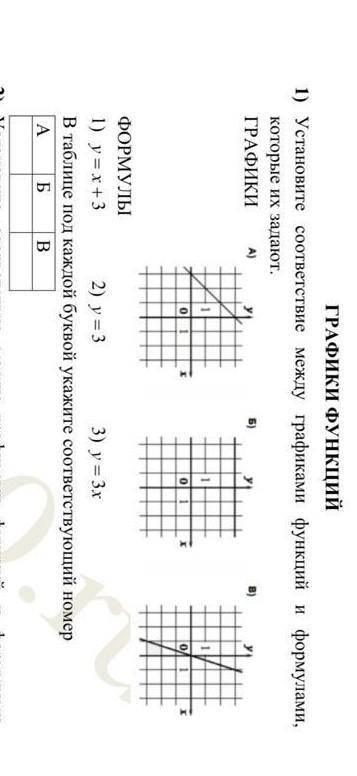
Под буквой А - 1, под буквой Б - 2 и под буквой В - 3