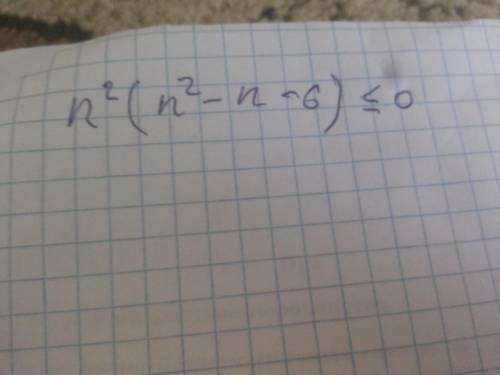
n²(n²-n-6)≤0
найдем корни левой части.
n=0; по Виету n=3: n=-2.
-203
+ - - +
х∈[-2;3], сумма натуральных, входящих в ответ , 1+2+3=6
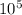в ней с единице 6 цифр , используем его 
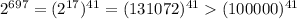а в числе 
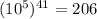цифр то есть в нашем чисел более 
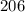цифр . 
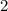в ней вероятность попадания четных чисел большая . 
и ее периодичность в среднем встречается в 4 раза то мы знаем что цифр в числе больше 206 , я проверил точно их 216 , это не важно , тогда 216/4=54 цифр . Снизим нашу вероятность 216/10=21,6
.
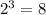то она может встречаться с вероятностью больше чем 4 других числа. 
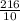<x
n²(n² - n - 6) ≤ 0
n²(n - 3)(n + 2) ≤ 0
+ - - +
[-2][0][3] n
n ∈ [- 2 , 3]
Натуральные числа принадлежащие этому отрезку : 1 ; 2 и 3 .
1 + 2 + 3 = 6
ответ : 6