
См. рисунок
1. Правильный шестиугольник, состоит из шести равносторонних треугольников.
Найдем сторону шестиугольника AB=r=48/6=8м.
Рассмотрим ΔСDO в нем CD=DO=0,5a (где а - сторона квадрата) ⇒ a=2CD
По теореме Пифагора найдем СD
r²=CD²+DO²=2CD² ⇒ r=CD√2⇒ м
м
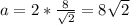 м
м
2. Из задачи №1. мы убедились, что радиус описанной окружности равен стороне правильного шестиугольника.
Площадь правильного шестиугольника равна
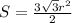 ⇒
⇒
 см
см
Длина окружности равна L=2πr=2π4√3=π*8√3≈43,5 см
3. Площадь сектора равна
 ≈151 см²
≈151 см²
(где n - градусная мера дуги сектора)

Объяснение:
Как я понял, задача состоит в нахождении наибольшего значения функции. Для это необходимо найти производную этой функции и приравнять ее к 0 .
Правила взятия производной, необходимые для решения этого примера:
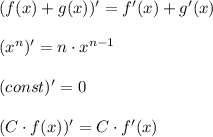
Эти правила можно описать следующим образом :
· Производная от суммы функций равна сумме их производных.
· Производная степенной функции равна произведению показателя степени на функцию, с показателем степени на 1 меньше исходного.
· Производная от постоянной величины равна 0.
· Постоянный множитель можно вынести за знак производной.
Тогда производная заданной функции равна :
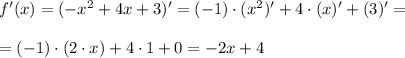
Приравняем производную к 0 и найдем корень уравнения:
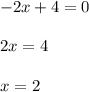
Подставим найденное значение в исходную функцию:
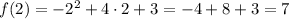
Получили, что наибольшее значение функции равно 7 в точке x=2
Объяснение:в приложении