ответ: 3
Объяснение:
Последняя цифра числа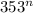 
чередуется как последняя цифра 
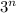и чередуется по правилу: 
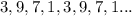(Чтобы понять на что оканчивается цифра 
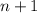- й степени, достаточно умножить исходную цифру на 3 и записать цифру, на которую оканчивается результат)
Период повторений равен 4.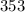 
при делении на 4 дает остаток 1, а значит кончается на первую цифру в периоде, то есть на 3.
Число делится на 5, только когда оно кончается на 0 или 5, а значит остаток от деления на 5 числа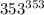 
равен 3.
2) {x+y=5
{x^3 +y^3=35
1.Из 1-го уравнения выразим х через у: х=5-у
2. Подставим во 2-е уравнение полученное выражение:
(5-у)^3+y^3 = 35
125 - 75y+15y^2-y^3+y^3=35
15y^2-75y+90=0
y^2-5y+6=0
Подберём корни по теореме обратной теореме Виета
у1=2, у2=3
3. Найдём х1 и х2
х1= 5-2=3 х2=5-3=2
(3;2) и (2;3)
3) {3x=y+1
{7^y-2x+2=7^y-4x+1+6
1. Выразим из 1-го у через х: у=3х-1
2. Подставим во 2-е предварительно упростив его
7^y-2x+2=7^y-4x+1+6,
7^y-2x-7^y+4x=-2+1+6
2х=5
х=2,5
3. Найдём у: у=3х-1=3*2,5-1=7,5-1=6,5
ответ. (2,5;6,5)
в) Преобразуем числитель. (1-cos²x+sin²x)/(x*tg3x)=2sin²x/(x*tg3x), подведем данную запись под первый замечательный предел. При икс, стремящемся к нулю, sinx ; tg3x эквивалентны х и 3х соответственно, а потому получим предел дроби 2*х*х/(х*3х) и он равен 2/3.
ответ 2/3
г) преобразуем (4-x)*(㏑(2-3х)-㏑(5-3х))=(4-x)*(㏑((2-3х)/(5-3х))=
(4-x)㏑((3х-2)/(3х-5))=(4-x)㏑((1+3/(3x-5))=㏑((1+3/(3x-5))^(4-x)
cвели решение ко второму замечательному пределу, возьмем сначала предел от (1+3/(3x-5))^(4-x), а затем логарифм от полученного предела.
представим (1+3/(3x-5))⁽⁴ ⁻ˣ⁾=(((1+(3/(3x-5)))⁽³ˣ ⁻⁵⁾/³))⁽³⁽⁽⁴⁻ˣ⁾/⁽³ ˣ⁻⁵)предел от этого выражения равен е⁻¹, а ㏑е⁻¹=-1*lnе=-1
ответ -1
353 - оканчивается на 3
353²=9 - оканчивается на 9
353³=7 - оканчивается на 7
353⁴=1 - оканчивается на 1
...
цикл повторяется.
353³⁵³=353³⁵²·353
353³⁵²=(353⁴)⁸⁸ - оканчивается на 1
353³⁵³=353³⁵²·353 - оканчивается на 3
353³⁵³:5= число, которое оканчивается на 0 ( остаток 3)