Question

Решить уравнения:
1) 28x³+3x²+3x+1=0
2) (x²+4x)(x²+x-6)=(x³-16x)(x²-2x-35)

Answer 1

1-ое уравнение:

$x=-\dfrac{1}{4}$

2-ое уравнение:

$x_1=0\\x_2=-4\\x_3=-2\sqrt{\dfrac{133}{9}}\cos\left(\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}\right)+\dfrac{7}{3}\\x_4=-2\sqrt{\dfrac{133}{9}}\cos\left(\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}+\dfrac{2\pi}{3}\right)+\dfrac{7}{3}\\x_5=-2\sqrt{\dfrac{133}{9}}\cos\left(\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}-\dfrac{2\pi}{3}\right)+\dfrac{7}{3}\\$

Объяснение:

$28x^3+3x^2+3x+1=0$

разложение на множители):

Заметим, что данное уравнение хорошо раскладывается на множители:

$28x^3+3x^2+3x+1=28x^3+7x^2-4x^2-x+4x+1=\\=7x^2(4x+1)-x(4x+1)+(4x+1)=(4x+1)(7x^2-x+1)=0$

Второй множитель не имеет корней.

Поэтом ответ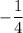 $-\dfrac{1}{4}$.

Поделим исходное уравнение на 28. Получим:

$x^3+\dfrac{3}{28}x^2+\dfrac{3}{28}x+\dfrac{1}{28}=0$, где $a=\dfrac{3}{28},\;b=\dfrac{3}{28},\;c=\dfrac{1}{28}$

Выполним вычисления:

$Q=\dfrac{a^2-3b}{9}=-\dfrac{27}{784}\\R=\dfrac{2a^3-9ab+27c}{54}=\dfrac{351}{21952}\\S=Q^3-R^2\approx-0.0003\\\varphi =\dfrac{1}{3}\times \mathrm{Arsh}\left(\dfrac{|R|}{\sqrt{|Q|^3}}\right)=\dfrac{1}{2}\ln3$

Тогда действительный корень будет равен:

$x=-2\sqrt{\dfrac{27}{784}}\mathrm{sh}\left(\dfrac{1}{2}\ln 3\right)-\dfrac{1}{28}=-\dfrac{1}{4}$

Пришли к тому же ответу.

Уравнение решено!

2)

(x²+4x)(x²+x-6)=(x³-16x)(x²-2x-35)

Раскроем скобки и упростим вырождение:

$x^5-3x^4-56x^3+34x^2+584x=0\\\\x=0\\x^4-3x^3-56x^2+34x+584=0$

Второе уравнение раскладывается на множители:

$(x+4)(x^3-7x^2-28x+146)=0\\\\x=-4\\x^3-7x^2-28x+146=0$

Последнее кубическое уравнение не имеет целых корней.

Поэтому нужно считать так же, как мы делали это при решении 1-ого уравнения 2-ым

$x^3-7x^2-28x+146=0\\\\Q=\dfrac{133}{9}\\R=\dfrac{746}{27}\\S\approx24640$

Значит имеем 3 корня:

$\varphi=\dfrac{1}{3}\arccos(\dfrac{R}{\sqrt{Q^3}})=\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}$

$x_1=-2\sqrt{\dfrac{133}{9}}\cos\left(\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}\right)+\dfrac{7}{3}\\x_2=x=-2\sqrt{\dfrac{133}{9}}\cos\left(\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}+\dfrac{2\pi}{3}\right)+\dfrac{7}{3}\\x_3=x=-2\sqrt{\dfrac{133}{9}}\cos\left(\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}-\dfrac{2\pi}{3}\right)+\dfrac{7}{3}$

Итого, уравнение имеет 5 корней:

$x_1=0\\x_2=-4\\x_3=-2\sqrt{\dfrac{133}{9}}\cos\left(\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}\right)+\dfrac{7}{3}\\x_4=-2\sqrt{\dfrac{133}{9}}\cos\left(\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}+\dfrac{2\pi}{3}\right)+\dfrac{7}{3}\\x_5=-2\sqrt{\dfrac{133}{9}}\cos\left(\dfrac{\arccos\left(\dfrac{746\sqrt{133}}{17689}\right)}{3}-\dfrac{2\pi}{3}\right)+\dfrac{7}{3}\\$

Задание выполнено!