2x^2+9x-5=0
D=b^2-4ac=9^2-4*2(-5)=81+40=121 -корень-11
x1,2= -b+\-корень из D / 2a= -9+\-11 / 4= -5 ; 0,5
(х+3)(5х-3)=05x^2+12x-9=0
D=k^2-ac=6^2-5*(-9)=36+45=81 -корень-9
x1,2= -k+\-корень из D / a= -6+\-9 / 5= -3 ; 0,6
(4у-3)(5-8у) =0-32y^2+44y-15=0 | *(-1) __ 32y^2-44y+15=0
D=k^2-ac=(-22)^2-32*15=484-480=4 -корень-2
x1,2= -k+\-корень из D / a= 22+\-2 / 32= 0,625 ; 0,75
(6а+5)(а-8)=06a^2-43a-40=0
D=b^2-4ac=(-43)^2-4*6(-40)=1849+960=2809 -корень-53
x1,2= -b+\-корень из D / 2a=43+\-53 / 12= -5\6 ; 8
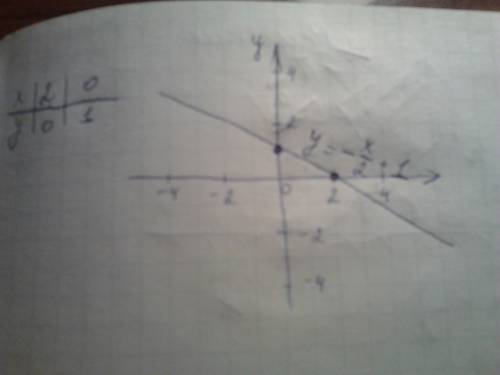
График на фотографии.
А) Найдем наибольшее и наименьшее значение функции на отрезке [-4;6]. Так как графиком функции является прямая, которая убывает на R, то для нахождения наибольшего и наименьшего значений достаточно подставить в функцию крайние точки промежутка.
у(-4) = (-1/2)*(-4) + 1 = 3
у(6) = (-1/2)*6 + 1 = -2
Значит, у наиб = 3, у наим = -2.
Б) -1/2x + 1 > 0
-1/2x > -1
х < 2.
у > 0 на промежутке (- бексконечность; 2)
ИЛИ
по графику видно, что у > 0 на промежутке (- бексконечность; 2)
10^6
Объяснение:
10^-4*(0,01)^-5=10^-4*10^10=10^6