ответ:пусть х=0
4*0 + 3y =12
3y =12
y=12:3
y=4
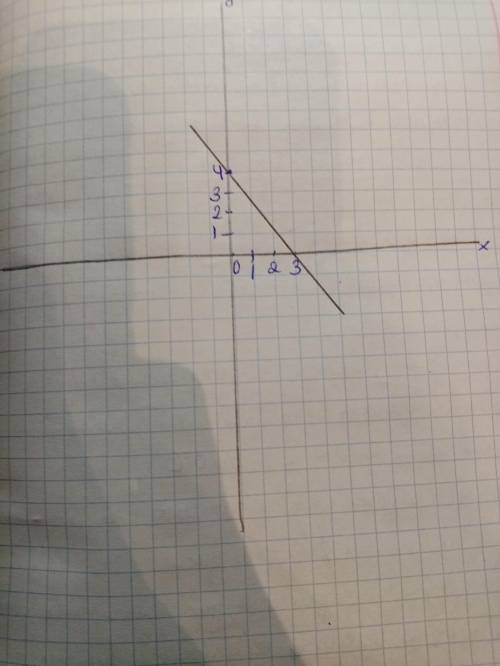
(0;4)
Пусть у= 0
4х + 3*0=12
4х=12
Х=12:4
Х=3
(3;0)
Объяснение:
Есть 12 вариантов выбора книг для покраски по количеству книг в каждом цвете (красный, зеленый, коричневый)
1 1 10
1 2 9
1 3 8
1 4 7
1 5 6
2 2 8
2 3 7
2 4 6
2 5 5
3 3 6
3 4 5
4 4 4
Им соответствуют количество вариантов выбора книг по их числу, например, первому, 12!/(10!*2!)*2!/(1!*1!)=66*2=132. Их надо посчитать.
И каждому набору соответствует число возможных перестановок по цветам. Если все числа в наборе разные, то 3!=6, если две одинаковые, до 3!/(2!*1!)=3, если все одинаковые (последний случай) , то 3!/(3!*0!)=1.
Затем количество вариантов выбора книг для каждого набора надо умножить на количество перестановок в наборе (то есть, для первого получится 132*3=396), и полученные числа сложить. Получится 519156.
1.1.D(y)=[-5;4]
2.Е(у)=[-1;3]
3.Нули функции х=-3; х=3.5
4. Промежутки знакопостоянства. у>0 при х∈[-5;-3)∪(-3;3.5)
y<0 при х∈(3.5; 4]
5. Функция возрастает при х∈[-3;1] и убывает при х∈[-5;-3];[1;4]
6. Наибольшее значение у=3; наименьшее у=-1
7.Ни четная, ни нечетная.
8 Не периодическая.
2. f(10)=100-80=20
f(-2)=4+16=20
f(0)=0
5. 1.D(y)=(-∞;+∞)
2.Е(у)=(-∞;-1]
3.Нули функции нет
4. Промежутки знакопостоянства. у>0 ни при каких х, а при х∈(-∞;+∞)
y<0
5. Функция возрастает при х∈(-∞;-3] и убывает при х∈[-3;+∞)
6. Наибольшее значение у=-1; наименьшего нет
7.Ни четная, ни нечетная.
8 Не периодическая.
График проходит через точки 3 по оси х и через точку 4 по оси у