Объяснение:

Метод Гаусса.
Запишем систему в виде расширенной матрицы:

Добавим 2-ю строку к 1-й, предварительно умножив 2-ю строку
на (-1):

Добавим 3-ю строку ко 2-й, предварительно умножив 2-ю строку
на 4, а 3-ю строку на (-1):

Добавим 4-ю строку к 3-й, предварительно умножив 4-ю строку
на (-2):

Добавим 2-ю строку к 1-й, предварительно умножив 2-ю строку
на 2:

Добавим 3-ю строку ко 2-й, предварительно умножив 3-ю строку
на (-1):

Добавим 2-ю строку к 1-й, предварительно умножив 1-ю строку
на 12, а 2-ю строку на (-19):

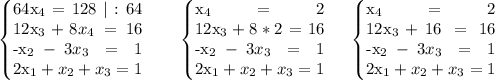
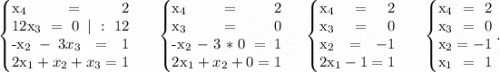
ответ: x₁=1 x₂=-1 x₃=0 x₄=2.
Конкретное преобразование зависит от цели.
Например, можно перейти к функциям только одинарного угла. Для этого применим формулу синуса двойного угла:
Используя полученное выражение и основное тригонометрическое тождество можно получить выражение только через синус или только через косинус:
Можно было перейти к выражению через косинус двойного угла с основного тригонометрического тождества:
Или же воспользоваться формулой понижения степени (половинного угла):