
![x^2-5\left | x \right |+6\leq 0\\\left | x^2 \right |-5\left | x \right |+6\leq 0\\\left ( \left | x \right |-2 \right )\left ( \left | x \right |-3 \right )\leq 0\\\left ( \left | x \right |-2 \right )\left ( \left | x \right |+2 \right )\left ( \left | x \right |-3 \right )\left ( \left | x \right |+3 \right )\leq 0\\\left ( x^2-4 \right )\left ( x^2-9 \right )\leq 0\\\left ( x-2 \right )\left ( x+2 \right )\left ( x-3 \right )\left ( x+3 \right )\leq 0\\x\in \left [ -3;-2 \right ]\cup \left [ 2;3 \right ]](/tpl/images/3785/0862/8293a.png)
а) f(x) = x/5 + 1
x/5 + 1 < 0 ⇒ x/5 < -1 ⇒ x < -5
f(x) < 0 при х ∈ (-∞; -5)
f(x) = 0 при х = -5
f(x) > 0 при х ∈ (-5 ; +∞)
б)
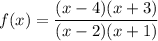
Решаем задачу методом интервалов
1) находим точки нулевых значений функции
х - 4 = 0 ⇒ х = 4
х + 3 = 0 ⇒ х = -3
2) находим точки разрыва функции
х - 2 = 0 ⇒ х = 2
х + 1 = 0 ⇒ х = - 1
Делим числовую прямую на интервалы и определяем знаки функции в этих интервалах
---( + )-------- -3 ---( - )-------- -1 ----( + )---------- 2 ----( - )---------- 4 ------(+) ----------
f(x) < 0 при х ∈ (-3; -1)∪(2; 4)
f(x) > 0 при х ∈ (-∞; -3)∪(-1; 2)∪(4; +∞)