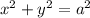
..............................
Рассмотрим левую часть равенства - сумму двух квадратов. Так как квадрат принимает только неотрицательные значения, то и их сумма будет неотрицательной. Таким образом, левая часть равенства неотрицательна. Значит, и правая часть равенства неотрицательна.
В правой части записан квадрат. Квадрат, в том числе и по указанным выше причинам, неотрицателен. Но если квадрат числа принимает неотрицательные значения, то само число может быть и отрицательным, так как отрицательное число в квадрате дает положительное.
Значит, каких-либо ограничений на 
нет. Параметр может принимать любые значения.
у = -2х + 1
Объяснение:
f(x) = - х2 + 2х – 3
g(x) = x2+ 2
Уравнение касательной к графику функции в точке х0 имеет вид:
у = f’(x0) (x – x0) + f(x0)
1. Составим уравнение касательной к графику f(x) = - х2 + 2х – 3:
Пусть касательная проходит через точку х0 = с:
f’(x) = (- х2 + 2х – 3)’ = - 2x + 2
f’(c) = -2c + 2
f(c) = - c2 + 2c – 3
Уравнение касательной:
у = (-2с + 2) (х – с) - c2 + 2c – 3 = -2сх + 2с2 + 2х - 2с - c2 + 2c – 3 = (2 - 2с)х + с2 – 3
у = (2 - 2с)х + с2 – 3
2. Составим уравнение касательной к графику g(x) = x2+ 2:
Пусть касательная проходит через точку х0 = а:
g’(x) = (x2+ 2)’ = 2x
g’(а) = 2а
g(а) = а2 + 2
Уравнение касательной:
у = 2а (х – а) + а2 + 2 = 2ах – 2а2 + а2 + 2 = 2ах - а2 + 2
у = 2ах - а2 + 2
3. Т.к. искомая касательная едина для двух функций, то
2 – 2с = 2а
с2 – 3 = - а2 + 2
Решим систему уравнений.
а = 1 – с
подставим во второе уравнение:
с2 – 3 = - (1 – с)2 + 2
с2 – 3 = - 1 + 2с – с2 + 2
с2 – 3 + 1 - 2с + с2 – 2 = 0
2с2 – 2с – 4 = 0
с2 – с – 2 = 0
(с + 1) (с - 2) = 0
с1 = - 1
с2 = 2
Тогда:
а1 = 2
а2 = - 1
Таким образом, графики функций имеют 2 общие касательные:
у = 4х – 2
у = -2х + 1
Выделите квадрат двучлена.
Объяснение:
1.
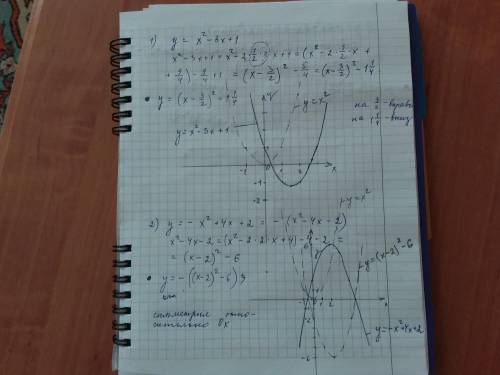
у=х^2-3х+1=(х^2-2×1,5х+1,5^2)-1,25=
=(х-1,5)^2-1,25
Строим график:
Шаг 1:
Строим график у=х^2.
Шаг 2:
Параболу перемещаем вдоль ОХ впра
во на 1,5ед.
Шаг 3:
Совершаем параллельный перенос
вдоль ОУ вниз на 1,25ед.
Построен искомый график.
2.
у=-х^2+4х+2
у=-(х^2-2×2х+2^2)+6=
=-(х-2)^2+6
Строим график:
Шаг 1:
Строим график у=х^2
Шаг 2:
Параболу перемещаем вдоль ОХ
вправо на 2ед. (ветви направлены
вверх).
Шаг 3:
Отражаем зеркально относитель
но ОХ (ветви параболы идут вниз).
Шаг 4:
Совершаем параллельный пере
нос вдоль ОУ вверх на 6ед.
Искомый график построен.