Длина первой окружности длиннее второй в 10 раз
Объяснение:
R1=15
R2=1,5
D1=30
D2=3
30:3=10
Длина окружности прямо пропорциональна длине диаметра (D)и длине радиуса (R)
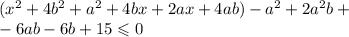
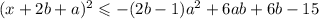
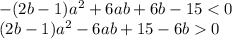
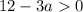
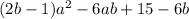 должен принимать только положительные значения. Как известно, так будет, если: 1. Коэффициент при a^2 положительный и 2. Дискриминант отрицательный.
должен принимать только положительные значения. Как известно, так будет, если: 1. Коэффициент при a^2 положительный и 2. Дискриминант отрицательный.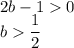
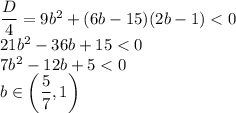
в 10 раз больше
Объяснение:
15:1,5=10