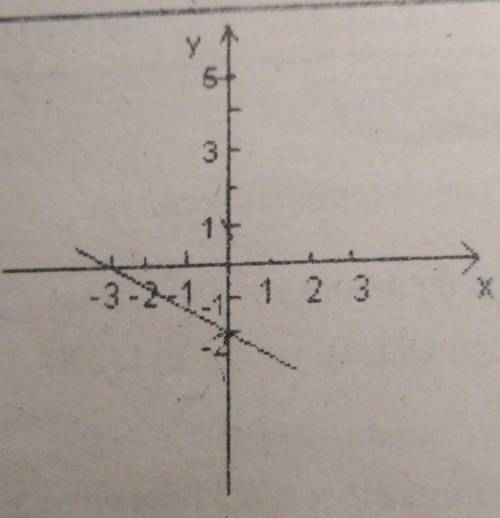
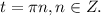 Если перебрать целые значения n, то получим числа:
Если перебрать целые значения n, то получим числа: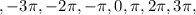 ....Это точки числовой окружности отмеченные, начиная с 0 через
....Это точки числовой окружности отмеченные, начиная с 0 через 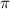 , (т е через полкруга). против часовой стрелки положительные значения, по часовой - отрицательные. Положительные значения из промежутка [0;2π] мы можем показать на окружности, таких значений два: 0 и
, (т е через полкруга). против часовой стрелки положительные значения, по часовой - отрицательные. Положительные значения из промежутка [0;2π] мы можем показать на окружности, таких значений два: 0 и 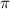 остальные будут совпадать с уже указанными, отрицательные значения из промежутка [-2π;0], их тоже два 0 и
остальные будут совпадать с уже указанными, отрицательные значения из промежутка [-2π;0], их тоже два 0 и 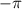 , для данной формулы тоже совпадут с уже указанными.
, для данной формулы тоже совпадут с уже указанными.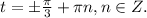 Это точки числовой окружности отмеченные, начиная с
Это точки числовой окружности отмеченные, начиная с 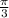 через
через 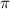 , (т е через полкруга) против часовой стрелки положительные значения, и начиная с
, (т е через полкруга) против часовой стрелки положительные значения, и начиная с  через
через 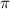 , (т е через полкруга) по часовой - отрицательные. И опять на промежутке [0;2π] мы можем показать на окружности только два значения:
, (т е через полкруга) по часовой - отрицательные. И опять на промежутке [0;2π] мы можем показать на окружности только два значения: 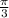 и
и 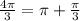 , остальные совпадут с уже указанными, и на промежутке [-2π;0] тоже два значения:
, остальные совпадут с уже указанными, и на промежутке [-2π;0] тоже два значения:  и
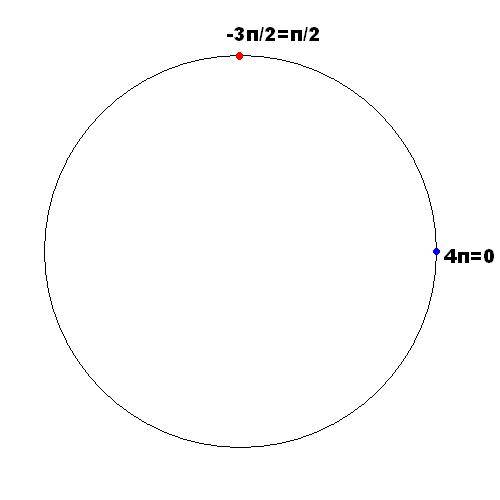
и 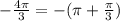 тоже совпадут с уже указанными.В целом мы отметили на окружности 4 точки:
тоже совпадут с уже указанными.В целом мы отметили на окружности 4 точки: 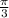 ,
, 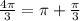 ,
,  ,
, 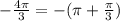 .
. 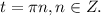 На промежутке [0;2π] два значения: 0 и
На промежутке [0;2π] два значения: 0 и 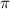 , остальные для
, остальные для 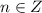 совпадут с уже указанными.
совпадут с уже указанными.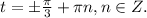 на промежутке [0;2π] два значения:
на промежутке [0;2π] два значения: 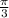 и
и 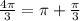 , на промежутке [-2π;0] тоже два значения:
, на промежутке [-2π;0] тоже два значения:  и
и 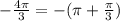 остальные для
остальные для 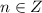 совпадут с уже указанными. Всего на окружности отмечено 4 точки:
совпадут с уже указанными. Всего на окружности отмечено 4 точки: 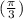 ,
, 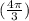 ,
, 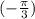 ,
, 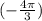 .
.
х=3k+1 или х =3k+2
y не делится на 3, значит дает в остатке либо 1 либо 2
y= 3n +1 или y =3n+2
тогда
а= (3k+1)⁴+(3n+1)⁴+1=(3k)⁴+4(3k)³+6(3k)³+4(3k)+1+(3n)⁴+4(3n)³+6(3n)³+4(3n)+1+1
Каждое слагаемое, которое содержит 3k или 3n кратно 3,
1+1+1=3 тоже делится на 3
или
а= (3k+2)⁴+(3n+2)⁴+1=(3k)⁴+4(3k)³·2+6(3k)³·2²+4(3k)·2³+16+(3n)⁴+4(3n)³·2+6(3n)³·2²+4(3n)·2³+16+1
Каждое слагаемое, которое содержит 3k или 3n кратно 3,
16+16+1=33 тоже делится на 3
или
а= (3k+1)⁴+(3n+2)⁴+1=(3k)⁴+4(3k)³+6(3k)³+4(3k)+1+(3n)⁴+4(3n)³·2+6(3n)³·2²+4(3n)·2³+16+1
Каждое слагаемое, которое содержит 3k или 3n кратно 3,
1+16+1=18 тоже делится на 3
или
а= (3k+2)⁴+(3n+1)⁴+1=(3k)⁴+4(3k)³·2+6(3k)³·2²+4(3k)·2³+16+(3n)⁴+4(3n)³+6(3n)³+4(3n)+1+1
Каждое слагаемое , которое содержит 3k или 3n кратно 3,
16+1+1=3 и тоже делится на 3