Укажите наименьшее значение параметра а при котором уравнение икс в кубе минус икс в квадрате плюс 12 - 3 a в квадрате равно нулю равно 3 различных уровнях
1) Используя формулу n-го члена арифметической прогрессии , вычислим двадцатый член этой прогрессии:
ответ: 30.
2) Формула суммы первых n членов арифметической прогрессии следующая:
Найдем же сначала восемнадцатый член арифметической прогрессии
ответ: 656.
3) Первый член:
Второй член:
Третий член:
Как видно, каждый последующий член уменьшается на (-5),т.е. это разность d = -5, следовательно, последовательность является арифметической прогрессией.
4) Используя n-ый член арифметической прогрессии, найдем ее разность
Да, является арифметической прогрессией.
5) Данная последовательность является арифметической прогрессии с первым членом и разностью прогрессии d=1
Всего таких членов не трудно посчитать по формуле n-го члена арифметической прогрессии:
То есть, нужно посчитать сумму первых 91 членов арифметической прогрессии
1) Найдите наименьшее значение ф-ии y = 5cos x + 6x + 6 на отрезке [0;3π/2] Решение Находим первую производную функции: y' = - 5sin(x) + 6 Приравниваем ее к нулю: - 5sin(x) + 6 = 0 Глобальных экстремумов нет Находим стационарные точки: Вычисляем значения функции на концах отрезка f(0) = 11 f(3/2) = 11 ответ: Имеются только локальные экстремумы (на заданном интервале) fmin = 11, fmax = 11
2) Найдите наименьшее значение ф-ии y = (x+6)^2(x+1) - 23 на отрезке [-7;-4] Решение Находим первую производную функции: y' = (x+1)(2x+12) + (x + 6)² или y' = 3x² + 26x + 48 Приравниваем ее к нулю: 3x² + 26x + 48 = 0 D = 676 - 4*3*48 = 100 x₁ = (- 26 - 10)/6 x₁ = - 6 x₂ = (- 26 + 10)/6 x₂ = - 8/3 Вычисляем значения функции на концах отрезка f(- 6) = - 23 f(- 8/3) = - 1121/27 f(- 7) = - 29 f(- 4) = - 35 ответ: fmin = -35, fmax = - 23
1) Используя формулу n-го члена арифметической прогрессии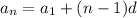 , вычислим двадцатый член этой прогрессии:
, вычислим двадцатый член этой прогрессии:
ответ: 30.
2) Формула суммы первых n членов арифметической прогрессии следующая: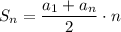
Найдем же сначала восемнадцатый член арифметической прогрессии
ответ: 656.
3) Первый член: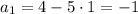
Второй член: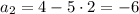
Третий член: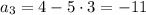
Как видно, каждый последующий член уменьшается на (-5),т.е. это разность d = -5, следовательно, последовательность является арифметической прогрессией.
4) Используя n-ый член арифметической прогрессии, найдем ее разность
Да, является арифметической прогрессией.
5) Данная последовательность является арифметической прогрессии с первым членом и разностью прогрессии d=1
и разностью прогрессии d=1
Всего таких членов не трудно посчитать по формуле n-го члена арифметической прогрессии:
То есть, нужно посчитать сумму первых 91 членов арифметической прогрессии
ответ: 4277.