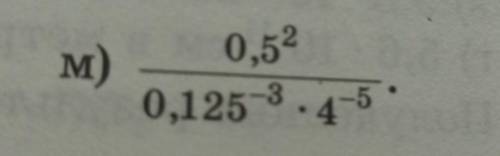
и 
. Чтобы найти для них общий знаменатель, нужно найти найменьшее общее число которое нацело делилось бы на знаменатель первого и второго дроба, в даном случае знаменатели это 25 и 4. Ну можно взять больший знаменатель умножить на 2 и проверить делится ли это число нацело на первый и другой знаменатель, если не делится ужножаеш на 3 и проверяеш, и так далее. Часто бывает, что один с знаменателей уже делится на себя и на второй знаменатель, тогда это и будет общий знаменатель. Потом оно само будет получаться, потому что будешь знать что на что делится.+ ;
;
= 
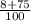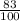, если можно сократить (то есть и числитель и множитель делится на одинаковое число), то сокращаем.
1) x²>4
При -2>х или х>2
ответ: Б.
2)х²+8х-9>=0
Введем функцию:
у=х²+8х-9 - график функции - парабола, ветви направлены вверх.
Найдем нули функции:
х²+8х-9=0
D=64+36=100
х1 = (-8-10)/2 = -9
х2 = (-8+10)/2 = 1
х∈(-беск.; -9]∪[1; +беск.).
ответ: Б.
3)3х²+5х-8<0
Введем функцию:
у=3х²+5х-8 - график функции - парабола, ветви направлены вверх.
Найдем нули функции:3х²+5х-8=0
D=25+96=121
x1 = (-5-11)/6 = -17/6 = -2 5/6
x2 = (-5+11)/6 = 1
х∈(-17/6;1)
Целые значения, которые входят в множество ответов: -2; -1; 0.
ответ: А.
4)
а)х²-14х+49>0
(х-7)²>0 - при х=7, неравенство не выполняется.
б)-3х²+х+2=<0
Введем функцию:
у=-3х²+х+2
Найдем нули функции:
-3х²+х+2=0
D=1+24=25 - 2 точки пересечения, значит, будет хотя бы одна точка выше оси х, неравенство не выполняется при всех х.
в)х²-3х+4>0
Введем функцию:
у=х²-3х+4
Найдем нули функции:
х²-3х+4=0
D=9-16= -7 - точек пересечения с осью х нет, при этом график функции - парабола с ветвями направленными вверх, то есть, при всех х, выполняется неравенство.
ответ: В.
5)f(x)= 5/√8x-4x²'
Найдем ОДЗ:
√8х-4х²' не= 0
8х-4х² не= 0
4х(2-х) не= 0
х не= 0; 2.
Область определения функции:
(-беск.;0)∪(0;2)∪(2;+беск.)
ответ: к сожалею, не все варианты ответов видны, но я уверен, что среди невидных ответов есть нужный.
0.5 = 1/2 = 2⁻¹
0,125 = 1/8 = 1/2³ = 2⁻³
4 = 2²
(2⁻¹)²/((2⁻³)⁺³*(2²)⁻⁵) = 2⁻²/(2⁹*2⁻¹⁰) = 2⁻² / 2⁻¹ = 2⁻²*2 = 2⁻¹ = 1/2