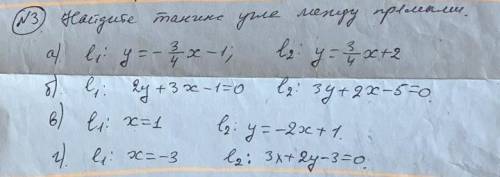
Угол φ между двумя прямыми, заданными уравнениями c угловыми коэффициентами
y=k₁x+b₁ y=k₂x+b₂, вычисляется по формуле: tgφ=(k₂-k₁)/(1+k₁*k₂)
а) y=-3х/4-1 и y=3х/4 +2
tgφ=(3/4+3/4)/(1-9/16)=3*16/(2*7)=24/7=3 3/7
б) 2y+3x-1=0 и 3y+2x-5=0; у=-3х/2 -1/2и у=2х/3 +5/3;
tgφ=(2/3+3/2)/(1-(3*2)*(2/3)); tgφ=∞; φ=90°
в) x = 1 и y = -2x + 1;
cosφ=(1*2+0*1)/(√1*√5)=2/√5; sinφ=√(1-4/5)=1/√5; tgφ=(1/√5):(2/√5)=1/2
г) x = -3 и 3x + 2y - 3 = 0
cosφ=(1*3+0*2)/(√1*√(3²+2²))=3/√13; sinφ=√(1-9/13)=2/√13;
tgφ=(2/√13):(3/√13)=2/3
Вначале необходимо найти производную и приравнять ее к 0 для нахождения экстремумов:
y' = (6cosx)' = -6*sinx = 0, sinx=0, x=pi/2 + pi*k
Дан промежуток [-pi/2; 0], необходимо определить, какие именно точки из множества решений попадают в него:
k=-1, x=pi/2-pi=-pi/2 - принадлежит промежутку
Является ли х=-pi/2 - экстремумом? - посчитать знак производной ДО и ПОСЛЕ этой точки: производная меняет свой знак с плюса на минус: х=-pi/2 - максимум функции.
На [-pi/2; 0] функция убывает, значит наибольшее значение y(-pi/2)=0, наименьшее значение y(0)=6
Объяснение:
Пусть х - скорость теплохода в неподвижной воде, тогда его скорость по течению равна х+4, а против течения х-4.
Время движения по течению 384/(х+4), время движения против течения 384/(х-4))
Составим уравнение 384/(х+4) +384/(х-4) + 8 = 48
96/(х+4) +96/(х-4) = 10
96х - 96*4 + 96х +96*4 = 10(х^2-16)
10 x^2 - 192x - 160 = 0
5 x^2 - 96x - 80 = 0
D =96^2 +4*80*5 = 9216 + 1600 = 10816, sqrt(D) = 104
x1 = (96+104)/10 = 20
x2 = (96-104)/10 <0 отрицательной скорости не может быть
ответ: скорость теплохода в неподвижной воде равна 20км/ч
Так как для прямой х=const (x=1) угол между прямой и осью ОХ равен 90° , а tg90° не существует, то указать угловой коэффициент прямой невозможно (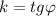 ) .
) .