В решении.
Объяснение:
Задание 1.
Известно, что график функции f(x) проходит через точку (−5; 3) и параллелен графику функции y = −4x + 3.
а) Найдите уравнение данной функции f(x) ( ).
Графики линейных функций параллельны, если k₁ = k₂, а b₁ ≠ b₂.
k₁ = -4, значит, k₂ = -4;
Вычислить b₂:
Подставить в уравнение известные значения х и у (координаты точки) и вычислить b₂:
3 = -4 * (- 5) + b₂:
3 = 20 + b₂:
3 - 20 = b₂:
b₂ = -17;
Уравнение второй функции:
у = -4х - 17.
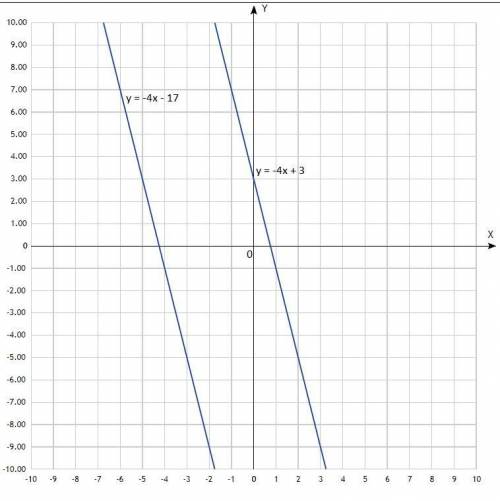
б) Постройте график данной функции f(x) ( ).
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
y = −4x + 3 у = -4х - 17
Таблицы:
х -1 0 1 х -6 -5 -4
у 7 3 -1 у 7 3 -1
По вычисленным точкам построить графики.
1 x0=5 у0=-2
похоже на у=3х² график сдвинут на -2 по оси у и на 5 вправо по оси х
2 х0= -1 у0= 3
похоже у=-2х² сдвинут вверх на 3 и на -1 влево
3 х0=0 у0= -1
похож на у=2х² сдвинут вниз на -1
4 х0=5 у0=0
похож на у=х² сдвинут вправо на 5
х0 можно найти и по формуле для ах²+вх+с=0 х0= -в/2а
например, у=3(х-5)²-2 =3x²-30x+73 a=3 b= -30 x0= -b/2a=30/6=5
y0=y(5)= -2
Объяснение: