Объяснение:
Первая система линейных уравнений:
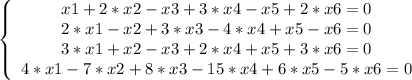
1-ое уравнение умножаем на -2 и складываем со 2-ым уравнением.
1-ое уравнение умножаем на -3 и складываем с 3-им уравнением.
1-ое уравнение умножаем на -4 и складываем с 4-ым уравнением.
Получаем нули при x1 во всех уравнениях, кроме 1-го:
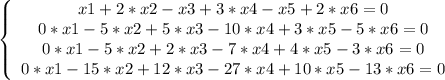
2-ое уравнение умножаем на -1 и складываем с 3-им уравнением.
2-ое уравнение умножаем на -3 и складываем с 4-ым уравнением.
Получаем нули при x2 во всех уравнениях, кроме 1-го и 2-го:
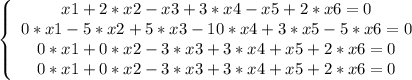
3-ье и 4-ое уравнения получились одинаковыми, 4-ое отбрасываем:
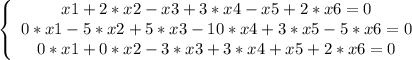
Получилась система, из которой можно получить фундаментальное решение:
x4, x5, x6 ∈ R
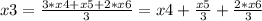
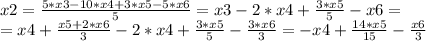
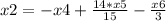
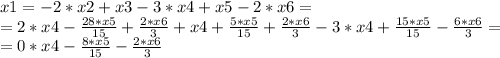
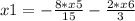
Вторая система решается точно также.
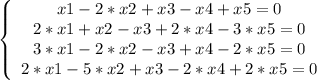
1-ое уравнение умножаем на -2 и складываем со 2-ым уравнением.
1-ое уравнение умножаем на -3 и складываем с 3-им уравнением.
1-ое уравнение умножаем на -2 и складываем с 4-ым уравнением.
Получаем нули при x1 во всех уравнениях, кроме 1-го:
4-ое уравнение ставим 2-ым, от этого система не меняется:
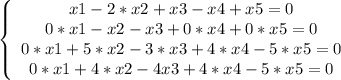
2-ое уравнение умножаем на 5 и складываем с 3-им уравнением.
2-ое уравнение умножаем на 4 и складываем с 4-ым уравнением.
Получаем нули при x2 во всех уравнениях, кроме 1-го и 2-го:
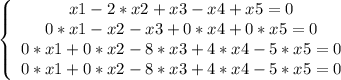
3-ье и 4-ое уравнения получились одинаковыми, 4-ое отбрасываем:
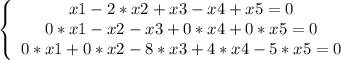
Получилась система, из которой можно получить фундаментальное решение:
x4, x5 ∈ R
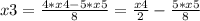
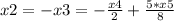
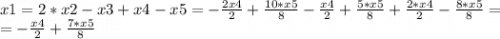
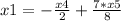
S = b1/(1 - q)
У нас b1 = 8, q = 0,5, S = 8/(1 - 0,5) = 16
2) Арифметическая прогрессия
a(n) = a1 + d*(n - 1)
У нас a1 = 3, d = 4, n = 10, a(10) = 3 + 4*9 = 3 + 36 = 39
3) b1 = 9, q = -1/3, S = 9/(1 - 1/3) = 9/(2/3) = 9*3/2 = 13,5
4) Сумма арифметической прогрессии
S = (a1 + a(n))*n/2
a1 = 2, n = 102-2+1 = 101, a(101) = 102
S = (2 + 102)*101/2 = 52*101 = 5252
5) a1 = -3, d = -3, n = 25, a(25) = -3 - 3*24 = -3 - 72 = -75
6) a1 = 10, d = -2, n = 10, a(10) = 10 - 2*9 = 10 - 18 = -8
S(10) = (10 - 8)*10/2 = 2*10/2 = 10