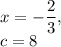
Объяснение:
Согласно теорему Безу, значение многочлена в точке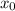 
равно остатку от деления многочлена на 
.
Так как мы знаем, что -4 -- корень уравнения, то остаток от деления многочлена на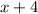 
равен 0. Запишем получившееся равенство:
.
Получили, что наш многочлен равняется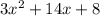 
.
Далее, для того, чтобы найти второй корень уравнения, можно поделить многочлен на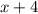 
в столбик, можно использовать теорему Виета, можно просто решить через дискриминант.
Как бы Вы не решали, многочлен раскладывается следующим образом:
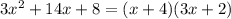
Значит второй корень: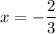 
(2а-5)^2-(2a-5)(2a+5) = (4a^2-20a+25)-(4a^2-10a+10a-25) = 4a^2-20a+25-4a^2+10a-10a+25 = -20a+50 = -20*1.5+50 = -30+50 = 20