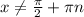
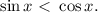
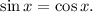Решать его можно, деля на косинус и получая при этом уравнение относительно тангенса. Но проще вспомнить, что косинус и синус - это абсцисса и ордината точки на единичной окружности. Они равны на биссектрисе 1-го и 3-го координатных углов. Меньше же ордината будет ниже этой прямой,чему соответствуют промежутки от 
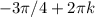до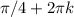 
.
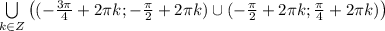
29.
б) в числителе выносим за скобку 5, получаем :
5(3b + 4c) / 10b
Сокращаем 5 и 10 на 5, получаем :
3b + 4c / 2b
г) В знаменателе выносим за скобку 6, получаем :
5x (y+2) / 6 (y + 2)
Сокращаем скобки (y+2) , получаем:
5x / 6
д) В знаменателе выносим за скобку a , получаем:
a - 3b / a(a-3b)
Сокращаем a-3b , получаем :
1 / a
30.
б) В числителе выносим 5 за скобку, а в знаменателе раскрываем формулу разности квадратов , получаем:
5(x - 3y) / (x-3y)(x+3y)
Сокращаем скобки (x-3y), получаем:
5 / x + 3y
г) В числителе выносим за скобку 6c , знаменатель не меняем, получаем:
6c(d-3) / (d-3)^2
Сокращаем скобки (d-3), получаем:
6c / d - 3
Формула разности квадратов :
x^2 - y^2 = (x-y) * (x+y)
y = 3x^2 + 6x -- это парабола.
a = 3, b = 6
Вершина параболы находится по формуле:
Xверш. = -b/2a = -6/2*3 = -1
Yверш. = 3*(-1)^2 + 6*(-1) = 3 - 6 = -3
Найдем точки пересечения с осями:
х = 0, y = 0
(0;0) -- точка пересечения с осью Оу.
y = 0, 3x^2 + 6x = 0
3x*(x + 2) = 0
x = 0, x = -2
(0; 0) и (-2; 0) -- точки пересечения с осью Ох.
Найдем еще две точки:
x = 1, y = 3 + 6 = 9
x = -3, y = 3*(-3)^2 + 6*(-3) = 27 - 18 = 9