
Объяснение:
Итак, мы имеем дело с алгебраической дробью.
Давайте мы упростим числитель и знаменатель данной дроби.
Числитель:
10a^2 можно разложить на множители - 2 * 5 * a * a
25ab можно тоже разложить на множители - 5 * 5 * a * b
Знаменатель:
b можно вынести за скобку.
И в итоге все это выглядит так:
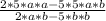
А теперь посмотрим в числитель дроби:
5a можно вынести за скобку, так как это число есть у обоих слагаемых.
А в знаменателе b вынесем за скобку по выше сказанной причине.
Получаем:
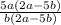
Мы числитель и знаменатель можем сократить на (2a-5b).
И в итоге получаем результат:
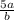
Подставляем данные нам значения в дробь:
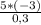
Получаем -15/0,3 = -150/3 = -50
ответ: -50
Задача решена.
ответ: Обратная функция - 
Область определения: 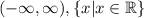
Область значений: 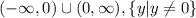
Объяснение: Нахождение обратной функции. Выразим одну переменную через другую.
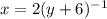
Решим относительно y.
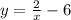
Решим относительно y и заменим на 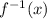 .
.

Нахождение областей определения и значения.
Областью определения выражения являются все вещественные числа, кроме тех, при которых выражение не определено. В данном случае нет вещественных чисел, при которых выражение было бы неопределенным.
Запись в виде интервала:
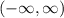
Нотация построения множества:
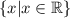
Область значений - это набор всех допустимых значений y. Используйте график для определения области значений.
Запись в виде интервала:
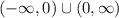
Нотация построения множества:
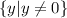
Определяем область определения и область значений.
Область определения: 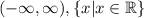
Область значений: 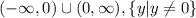
Объяснение:
Все вычисления в фото.
Внизу написано :