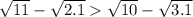Сравнить числовые значения выражений: П.с : я знаю, что можно возвести в квадрат, но мне нужно другим решить, так что РЕШИТЕ ДРУГИМ И КАК МОЖНО ПРЯМ ПОДРОБНО
Рассмотрим функцию . Она является возрастающей на всей области определения, то есть большему значению аргумента соответствует большее значение функции.
Рассмотрим числа и . Зная, что и в силу монотонности функции корня, получим, что .
Рассмотрим числа и . Зная, что и в силу монотонности функции корня, получим, что .
Обе части неравенства домножим на (-1), изменив знак неравенства:
Наконец, сложим два неравенства одного смысла и :
Другими словами, рассмотрев первое выражение и второе выражение , можно заключить следующее. Первое выражение имеет большее уменьшаемое, чем второе выражение. Также первое выражение имеет меньшее вычитаемое, чем второе выражение. Значит, первая разность больше второй.
Решаем уравнение, соответствующее данному неравенству: Тогда решением исходного неравенства будут промежутки меньше меньшего корня и больше большего: Второе неравенство не имеет решений, так как косинус не принимает значений больших 1. Первое неравенство удобно решить с тригонометрического круга. ответ: , где k - целые числа
Можно на всякий случай вводить замены такого рода: Тогда, Решаем с тригонометрического круга: ответ: , где k - целые числа
Значения табличные, но можно и на круге изобразить: ответ: , где k - целые числа
Решение на тригонометрическом круге: ответ: , где k - целые числа
Рассмотрим функцию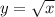 . Она является возрастающей на всей области определения, то есть большему значению аргумента соответствует большее значение функции.
. Она является возрастающей на всей области определения, то есть большему значению аргумента соответствует большее значение функции.
Рассмотрим числа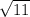 и
и 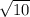 . Зная, что
. Зная, что 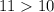 и в силу монотонности функции корня, получим, что
и в силу монотонности функции корня, получим, что 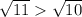 .
.
Рассмотрим числа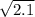 и
и 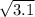 . Зная, что
. Зная, что 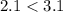 и в силу монотонности функции корня, получим, что
и в силу монотонности функции корня, получим, что 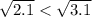 .
.
Обе части неравенства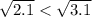 домножим на (-1), изменив знак неравенства:
домножим на (-1), изменив знак неравенства:
Наконец, сложим два неравенства одного смысла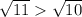 и
и 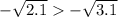 :
:
Другими словами, рассмотрев первое выражение и второе выражение
и второе выражение  , можно заключить следующее. Первое выражение имеет большее уменьшаемое, чем второе выражение. Также первое выражение имеет меньшее вычитаемое, чем второе выражение. Значит, первая разность больше второй.
, можно заключить следующее. Первое выражение имеет большее уменьшаемое, чем второе выражение. Также первое выражение имеет меньшее вычитаемое, чем второе выражение. Значит, первая разность больше второй.
ответ: