сумма n последовательных нечетных натуральных чисел при n>1
1+3+5+7+...+(2n-1)=n^2
Доказательство методом математической индукции
База индукции
n=2. 1+3=2^2
Гипотеза индукции
Пусть для n=k утверждение выполняется, т.е. выполняется
1+3+5+7+...+(2k-1)=k^2
Индукционный переход. Докажем, что тогда выполняется утверждение и для n=k+1, т.е, что выполняется
1+3+5+7+...+(2k-1)+(2K+1)=(k+1)^2
1+3+5+7+...+(2k-1)+(2K+1)=используем гипотезу МИ=k^2+(2k+1)=k^2+2k+1=используем формлу квадрату двучлена=(k+1)^2, что и требовалось доказать.
По методому математической индукции формула справедлива.
Число n^2 при n>1 zвляется составным, оно делится на 1,n,n^2.
А значит сумма n последовательных нечетных натуральных чисел при n>1 является составным числом. Доказано
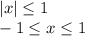
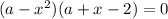
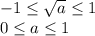
![a \in [0;1]](/tpl/images/0775/0492/4bfc3.png)
- неравенства будут иметь общее решение, значит при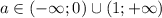 
неравенства общих решений не будет иметь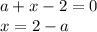
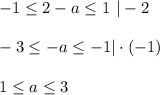
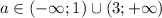неравенства общих решений не имеют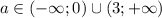
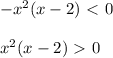
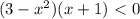
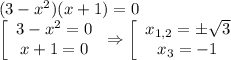
![a \in (-\infty;0]\cup[3;+\infty)](/tpl/images/0775/0492/a3d1e.png)
1)х=0
2)у=-1
3)z=-2
4)x=1,3
5)y=-5/3
6)x=-2