Question

При каких значениях параметра a квадратное уравнение x^2+ax+a-1=0 имеет 1 корень?

Answer 1

a=2, единственный корень x=-1

Объяснение:

При значении дискриминанта равного 0. Т.е.

a^2-4*(1)*(a-1)=0

a^2-4*a+4=0

Уже для этого уравнения дискриминант:

D = (-4)^2 - 4*1*4 = 16 - 16 = 0

a= 4/(2*1) = 2

Answer 2

Уравнение имеет единственный корень при 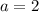$a=2$

Теория:

Стандартный вид квадратного уравнения 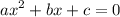${\displaystyle ax^2+bx+c=0}$

Его дискриминант равен ${\displaystyle D = b^2-4*a*c}$

А его корни равны:

${\displaystyle x = \frac{-b\pm\sqrt{D} }{2*a}}$

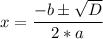
Объяснение:

Квадратное уравнение имеет один действительный корень тогда, когда его дискриминант равен нулю.

Для данного квадратного уравнения 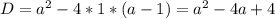$D = a^2 -4*1*(a-1) = a^2 -4a+4$

Получаем уравнение 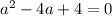$a^2 -4a+4=0$ Это обычное квадратное равнение.

Решаем через дискриминант:

$D=(-4)^2-4*1*4 = 16-16=0$

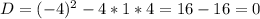
Данное квадратное уравнение имеет один действительный корень 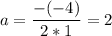${\displaystyle a = \frac{-(-4)}{2*1} = 2}$

Значит 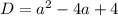$D = a^2 -4a+4$ равна нулю при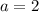 $a=2$

Следовательно уравнение 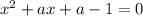$x^2+ax+a-1=0$ имеет один действительный корень при a = 2