Кролик со своим дядей может съесть одну морковь за 10 минут. дядя может съесть такую же морковь за 60 минут. за сколько времени такую же морковь может съесть кролик?
Надо исследовать функцию y, для этого найдем её производную.
График производной - парабола. Нам нужна точка минимума. Очевидно, что нужно знать точки экстремума. Заметим, что парабола всегда направлена вверх. Если парабола находится выше оси ОХ, точек минимума нет. Если касается, учитывая что в исходной функции 6x^3 (на бесконечности возрастает), то будет минимумом. Это условие D≥0
Далее, пусть - точки экстремума. На интервале функция будет убывать, то есть минимума своего достигнет в .
Найдем же эти точки в общем виде:
Теперь же невооруженным глазом видно, что дискриминант всегда больше 0, но докажем это всё-таки: при любых а.
Выразим точки экстремума:
Здесь независимо от значений а точка, где корень взят с "+" будет больше, а значит именно это значение будет точкой минимума.
Теперь подумаем над условием. В таком выражении и будет являться тем самым b. Подбирая любое b, получим выражение через а.
Но нужно ведь выразить а через b. Вернемся к уравнению y'=0
Выражаем а и получаем:
Ну а если через b, то
Но такое соответствие может быть и для точек локальных максимумов. Если значение точки минимума (т.е. то, что с "+" бралось) начать преобразовывать к удобоваримому виду, мы и получим уравнение y'=0, вот начало преобразований:
Уравнение вида
Вот как раз для точки минимума условие g(x)≥0 обязательно.
Вот надо решить это неравенство:
Ищем нули функции
В числителе
Раз D<0, то все выражение больше нуля из-за коэффициента при старшей степени, можно на него поделить без потерь и получить:
А х здесь это b.
То есть при
, где b - точка минимума.
А в остальных случаях для b значение a ему не будет соответствовать как то значение, где b - точка минимума.
Как-то. P.S. странное немного задание, может, я чего-то не понял))
Надо исследовать функцию y, для этого найдем её производную.
График производной - парабола. Нам нужна точка минимума. Очевидно, что нужно знать точки экстремума. Заметим, что парабола всегда направлена вверх. Если парабола находится выше оси ОХ, точек минимума нет. Если касается, учитывая что в исходной функции 6x^3 (на бесконечности возрастает), то будет минимумом. Это условие D≥0
Далее, пусть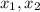 - точки экстремума. На интервале
- точки экстремума. На интервале 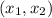 функция будет убывать, то есть минимума своего достигнет в
функция будет убывать, то есть минимума своего достигнет в 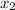 .
.
Найдем же эти точки в общем виде:
Теперь же невооруженным глазом видно, что дискриминант всегда больше 0, но докажем это всё-таки: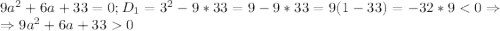 при любых а.
при любых а.
Выразим точки экстремума:
Здесь независимо от значений а точка, где корень взят с "+" будет больше, а значит именно это значение будет точкой минимума.
Теперь подумаем над условием. В таком выражении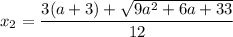 и будет являться тем самым b. Подбирая любое b, получим выражение через а.
и будет являться тем самым b. Подбирая любое b, получим выражение через а.
Но нужно ведь выразить а через b. Вернемся к уравнению y'=0
Выражаем а и получаем:
Ну а если через b, то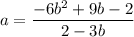
Но такое соответствие может быть и для точек локальных максимумов. Если значение точки минимума (т.е. то, что с "+" бралось) начать преобразовывать к удобоваримому виду, мы и получим уравнение y'=0, вот начало преобразований:
Уравнение вида
Вот как раз для точки минимума условие g(x)≥0 обязательно.
Вот надо решить это неравенство:
Ищем нули функции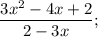
В числителе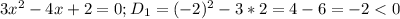
Раз D<0, то все выражение больше нуля из-за коэффициента при старшей степени, можно на него поделить без потерь и получить:
А х здесь это b.
То есть при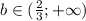
А в остальных случаях для b значение a ему не будет соответствовать как то значение, где b - точка минимума.
Как-то. P.S. странное немного задание, может, я чего-то не понял))