Графиком линейной функции является прямая.
х - независимая переменная, то есть может принимать любые значения.
у - зависимая переменная, то есть её значение зависит от значения х.
Чтобы построить график, возьмём две точки.
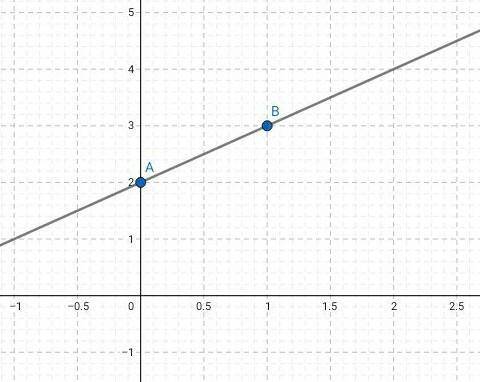
Если х = 0, у = 2
Если х = 1, у = 3
У нас есть координаты двух точек А (0;2), В (1;3). Теперь, построим график:
Задание#2А) Если х = 3 то у = 3 + 2 = 5
ответ: у = 5
Б) Если у = 0, то х:
0 = х + 2
-х = 2
х = -2
ответ: х = -2
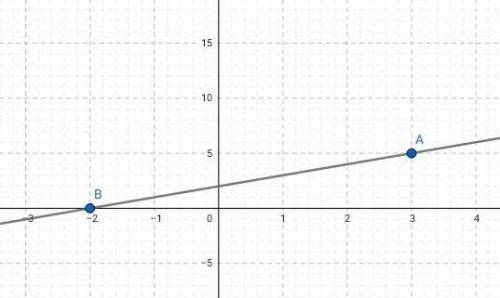
Если нужен график точек А (3;5) и В (-2;0), то он тоже прикреплен 2 картинкой.
Сначала разберём таблицу. В первой строке - значения выборки, вторая строка - показывает сколько раз каждое значение встречается в выборке. Таким образом полная выборка будет такой: 2; 5; 5; 5; 7; 7; 8; 8; 8; 8. Количество значений в выборке будет равно 10 (это обозначается так n = 10).
1) Среднее арифметическое = (2 · 1 + 5 · 3 + 7 · 2 + 8 · 4) / 10 = 6,3
2) Дисперсия обозначается S² и вычисляется по формуле: сумму разностей квадратов значения выборки и её среднего арифметического поделить на (n-1). Получаем
S² = ( (2 - 6,3)² + (5 - 6,3)² + (5 - 6,3)² + (5 - 6,3)² + (7 - 6,3)² + (7 - 6,3)² + (8 - 6,3)² + (8 - 6,3)² + (8 - 6,3)² + (8 - 6,3)² ) / 10 - 1 = 4,01
3) Среднее квадратическое отклонение обозначается буквой ω:
ω = √S² = √4,01 = 2,002
4) Мода - это значение встречающееся в выборке чаще других, то есть
мода = 8
Если выборка содержит нечетное количество элементов, медиана равна (n+1)/2-му элементу.
Если выборка содержит четное количество элементов (как в нашем случае), медиана лежит между двумя средними элементами выборки и равна среднему арифметическому, вычисленному по этим двум элементам. То есть
медиана = (7 + 7) / 2 = 7