70 км/ч
Объяснение:
Пусть х км/ч - скорость двухэтажного автобуса,
(х + 10) км/ч - скорость микроавтобуса.
Оба автобуса проехали по 280 км.
Запишем данные в таблицу, по строке выразим время движения каждого автобуса (расстояние разделить на скорость).
Время движения двухэтажного автобуса:
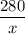ч
Время движения микроавтобуса:
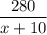ч
Известно, что туристы, ехавшие на двухэтажном автобусе, добрались до города на полчаса позже, т.е. время движения у них было больше на 0,5 ч. Вычитаем из большего времени меньшее и получаем уравнение:
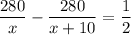
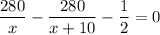
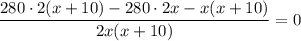
x > 0 по смыслу задачи, поэтому умножаем на знаменатель обе части уравнения.
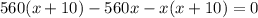
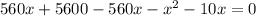
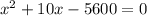
По теореме, обратной теореме Виета,
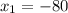- не подходит по смыслу задачи,
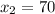(км/ч) - скорость двухэтажного автобуса.
y=1+x3, х∈(-∞;+∞) или D=(-∞;+∞)
y=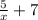
, х∈(-∞;0)∪(0;+∞) или D=(-∞;0)∪(0;+∞)
Объяснение:
Область определения функции - откуда до куда твой график существует по оси Х.
а) y=1+x3 график прямой х∈(-∞;+∞)
б) y=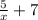
график гиберболы х∈(-∞;0)∪(0;+∞)
Если функция имеет вид: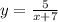
то х∈(-∞;-7)∪(-7;+∞)
Знаменатель х+7 говорит о том, что асимптота сдвинута по оси х влево.
Можно записывать ответ по разному, два варианта записи ответа, необходимо выбрать 1:
y=1+x3, (1вариант) х∈(-∞;+∞) или (2 вариант) D=(-∞;+∞)
y=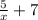
, (1вариант) х∈(-∞;0)∪(0;+∞) или (2 вариант) D=(-∞;0)∪(0;+∞)