Объяснение:
Эта задача имеет два принципиально разных решения.
А) считаем, что все голубые шары одинаковы между собой, и все розовые тоже одинаковы.
Тогда:
1) двумя : вынуть розовый шар или вынуть голубой шар.
2) тоже двумя : сначала вынуть розовый шар, потом голубой, или наоборот, сначала голубой шар, а потом розовый.
Б) считаем, что все шары разные, например, имеют номера, как в бильярде.
Тогда:
.
Допустим, мы первым вынимаем голубой шар. Это 6 разных .
За ним вынимаем розовый, это 8 разных .
Всего вынуть сначала голубой шар, потом розовый.
И ещё вынуть, наоборот, сначала розовый шар, потом голубой.
1)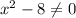
2)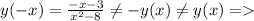 не является четной и нечетной
не является четной и нечетной
3)Горизонтальная:
y=0 - горизонтальная асимптота
Наклонная: y=kx+b
Наклонных нет
Вертикальная x = a, где а - точка разрыва
4)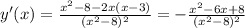
y' не сущ. при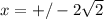
y' = 0 при х=2; х=4
- - + + -
-----------0-----------------.-----0---------.----------->x
-2sqrt(2) 2 2sqrt(2) 4
x = 2 - точка min y(2) = 1/4 - наименьшее значение
x = 4 - точка max y(4) = 1/8 - наибольшее значение
5)OX: y=0; x = 3 A(3;0)
OY: x=0; y=3/8 B(0;3/8)