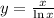
1. Область определения: На ноль делить нельзя -->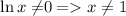 
и х не отрицательный т.к. х под натуральным логарифмом. Итоге: x∈[0;1)∪(1;+∞)
2. Функция общего вида т.к. f(-x)≠±f(x)
3. Точки пересечения с осями:
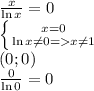Только одна точка (0;0)
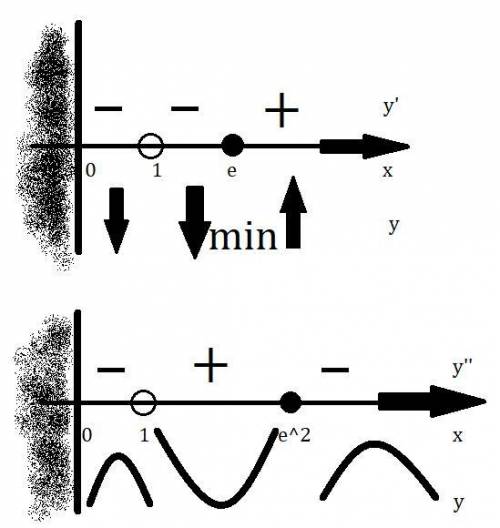
4. Исследование с 1ой производной:
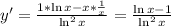
см. внизу.
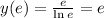
5. Исследование со 2ой производной:
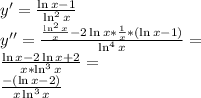
см. внизу.
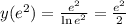
6. Асимптоты:
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: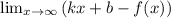 
Находим коэффициент k: 
Находим коэффициент b: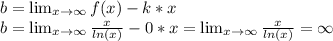 
Предел равен ∞, следовательно, наклонные асимптоты функции отсутствуют.
Найдем вертикальные асимптоты. Для этого определим точки разрыва: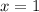 
Находим переделы в точке 1: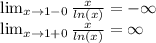 
Значит точка разрыва II рода и является вертикальной асимптотой.
48=3x умножить 4
48=12x^2
Делим всё это на 12:
48см^2=12x^2 |:12
4=x^2
Убираем квадрат и получаем x=+-2 (x^2 всегда будет положительным, т.к. это чётная степень. Поэтому x=2 и x=-2)
Но стороны не могут быть равны отрицательному значению, поэтому остаётся только 2.
Теперь находим стороны:
3x=6см
4x=8см
ответ: стороны прямоугольника равны 6см и 8см.