Возьмем за S весь объем задания, а за х и у - скорость первого и второго штукатура соответственно тогда первый может выполнить задание за S/x часов, а второй за S/y. S/x +5=S/y S/(x+y)=6 надо найти S/x и S/y
S/y-S/x=5 S=6x+6y S/x =6+6y/x S/y=6+6x/y 6+6y/x-6-6x/y=5 обозначим y/x=z 6z-6/z=5 6z²-6=5z 6z²-5z-6=0 D=5²+4*6*6=169 √D=13 z₁=(5-13)/12=-8/12=-2/3 отбрасываем, так как z не может быть отрицательным z₂=(5+13)/12=-18/12=3/2=1,5 S/x =6+6y/x=6+6z=6+6*1,5=6+9=15 S/y=6+6x/y=6+6/z=6+6/1,5=6+4=10 ответ: 15 и 10 часов
Выразим в первом уравнении переменную "у". Для этого нужно перенести неизвестную в правую часть и сменить ее знак. Получим:
Подставим данное значение "у" в уравнение "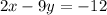
". Получим:
Рапределяем "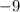
" через скобки. Получим:
Приводим подобные члены. Получим:
Переносим постоянную в правую часть и сменяем ее знак. Получим:
Вычисляем разность. Получим:
Делим обе стороны уравнения на "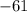
". Получим:
Подставляем данное значение "х" в уравнение "у=-19+7х". Получим:
Умножаем числа. Получим:
Вычисляем сумму. Получим:
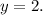
ОТВЕТ: решением данной системы уравнений является пара чисел "