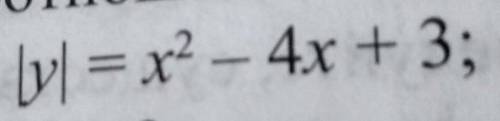
Объяснение:
1) f(x) = -x²-8x+9
f'(x)=(-x²-8x+9)'=-2x-8+0=-2x-8
f'(x)=0 при -2x-8=0 или -2х=8 или х=-4
f'(x) + -
о>
f(x). ↑. -4. ↓. x
функция возрастает при х є (-∞;-4),
функция убывает при х є (-4;+∞)
2) f(x) = -2x²+7x-5
f'(x)=(-2x²+7x-5)'=-4x+7+0=-4x+7
f'(x)=0 при -4x+7=0 или 4х=7 или х=1,75
f'(x) + -
о>
f(x). ↑. 1,75. ↓. x
функция возрастает при х є (-∞;1,75),
функция убывает при х є (1,75;+∞)
Решить систему линейных уравнений методом подстановки и методом сложения:
{
y
+
2
x
=
1
y
−
x
=
3
Решение методом подстановки.
{
y
+
2
x
=
1
y
−
x
=
3
⇒
{
y
=
−
2
x
+
1
y
−
x
=
3
⇒
{
y
=
−
2
x
+
1
(
−
2
x
+
1
)
−
x
=
3
⇒
{
y
=
−
2
x
+
1
−
3
x
−
2
=
0
⇒
{
y
=
−
2
x
+
1
x
=
−
2
3
⇒
{
y
=
7
3
x
=
−
2
3
y
=
2
1
3
;
x
=
−
2
3
Решение методом сложения.
{
y
+
2
x
=
1
y
−
x
=
3
Вычитаем уравнения:
−
{
y
+
2
x
=
1
y
−
x
=
3
(
y
+
2
x
)
−
(
y
−
x
)
=
1
−
3
3
x
=
−
2
x
=
−
2
3
Подставиим найденную переменную в первое уравнение:
(
−
2
3
)
+
2
x
=
1
y
=
7
3
y
=
2
1
3
;
x
=
−
2
3
Объяснение: