Наш многочлен имеет вид
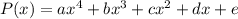
Пусть меньший его корень равен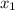 
. Так как корни образуют арифметичекую прогрессию, можем записать:
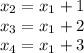
Многочлен раскладывается на линейный множители следующим образом:
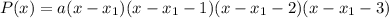
Напрашивается замена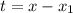 
. Тогда
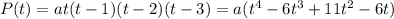
Нам нужно найти минимумы этой функции, поэтому дифференцируем:
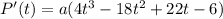
Теперь требуется найти корни этого многочлена. Используя теорему о рациональных корнях многочлена можно найти корень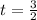 
Согласно теореме Безу,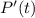 
должен делиться на 
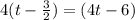. Разложим на множители, чтобы найти остальные корни:
![P'(t)=a(4t^3-6t^2-12t^2+18t+4t-6)=a[t^2(4t-6)-3t(4t-6)+(4t-6)]=a(4t-6)(t^2-3t+1)](/tpl/images/0952/7803/88744.png)
Решив квадратное уравнение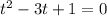 
, найдем корни
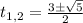
Расположив корни
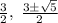
на числовой прямой и использовав метод интервалов, узнаем, что производная меняет знак с минуса на плюс в точках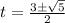 
, это и есть точки минимума. Переходя обратно к многочлену от x, получаем точки
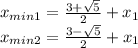
Квадрат расстояния между ними:
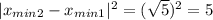
Пояснение решения:
В то время, когда часы показывают 19:30, минутная стрелка показывает на цифру 6, а часовая находится ровно посередине между цифрами 7 и 8 циферблата. Циферблат (360°) разделен цифрами на 12 равных частей, поэтому
360°:12=30° - градусная мера дуги между двумя соседними цифрами
циферблата
30°:2=15°- градусная мера половины дуги между двумя соседними
цифрами циферблата
30°+15°=45°- искомый угол между стрелками в 19:30
2) (cos45°-1)(cos45°+1)=cos²45°-1=(√2/2)²-1=1/2 -1= -1/2