MK и EF - медианы, а все три медианы пересекаются в одной точке. Поэтому если продолжить NO до пересечения с ME в точке L, отрезок NL будет третьей медианой. Как известно, медианы в точке пересечения делятся в отношении 2:1, считая от вершины. Поэтому MO=10; EO=12; OL - треть NL. Продолжим OL за точку L на отрезок OL; получаем точку A и четырехугольник MAEO, который является параллелограммом по признаку параллелограмма (диагонали в точке пересечения делятся пополам). Более того, он является прямоугольником, поскольку угол MOE прямой. В прямоугольнике диагонали равны, то есть AO=ME. А нужный нам отрезок ON равен AO. Остается применить теорему Пифагора:
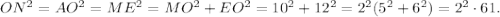
ответ: 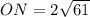
x=3 f’(3)=3*3^2-16*3=3*9-48=27-48=-21
2) f’(x)= [(-2x)* (x^2+7x+10) - (25-x^2)*(2х+7)]/ (x^2+7x+10)^2=
= [ (-2x)* (x+5)*(х+2) - (5-х)*(5+х)*(2х+7) ]/ [(x+2)(х+5)]^2=
= [ (-2x)*(х+2) - (5-х)*(2х+7) ]/ [(x+5)*(х+2)^2]=
= [ -2x^2 - 4х - 10х - 35 + 2х^2 + 7х ]/ [(x+5)*(х+2)^2]=
= [ -7х-35 ]/ [(x+5)*(х+2)^2]= [ -7*(х+5) ]/ [(x+5)*(х+2)^2]= -7/(х+2)^2
x=5 f’(5)= -7/(5+2)^2=-7/7^2=-1/7
3) f’(x)= [4x^3*(x^2-1) - (x^4-1)*2х]/ (x^2-1)^2=
=[4x^3*(x^2-1) - (x^2-1)*(х^2+1)*2х]/(x^2-1)^2= [4x^3 - (х^2+1)*2х]/(x^2-1)=
= [4x^3 - 2х^3-2х]/(x^2-1)=(2х^3-2х)/(х^2-1)=[2х*(х^2-1)]/( х^2-1)=2х
x=1 f’(1)= 2*1=2
4) f’(x)= [2х*(x-4) - (x^2-16)*1]/(х-4)^2= [2х*(x-4) - (x-4)*(х+4)]/(х-4)^2=
= [2х - (х+4)]/(х-4)=(2х-х-4)/(х-4)=(х-4)/(х-4)=1
x=4 f’(4)= 1
Конечно сокращение можно было выполнить сразу и тем упростить нахождение производной, но мне было удобней делать сокращения уже в производной.